Нормальная линейная модель парной (однофакторной) регрессии

Общий вид нормальной (традиционной или классической) линейной модели парной (однофакторной) регрессии (Classical Normal Regression Model):

yi=β0+β1xi+ε i ,

где yi – результативные переменные,

xi – факторные переменные,

β0, β1 – параметры модели регрессии, подлежащие оцениванию;

ε i – случайная ошибка модели регрессии.

При построении нормальной линейной модели парной регрессии учитываются пять условий:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии εi;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:

3) дисперсия случайной ошибки модели регрессии постоянна для всех наблюдений:

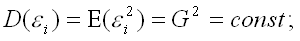
4) между значениями случайных ошибок модели регрессии в любых двух наблюдениях отсутствует систематическая взаимосвязь, т. е. случайные ошибки модели регрессии не коррелированны между собой (ковариация случайных ошибок любых двух разных наблюдений равна нулю): Cov(ε i,ε j)=E(ε i,ε j)=0 (). Это условие выполняется в том случае, если исходные данные не являются временными рядами;

5) на основании третьего и четвёртого условий часто добавляется пятое условие, заключающееся в том, что случайная ошибка модели регрессии – это случайная величина, подчиняющейся нормальному закону распределения с нулевым математическим ожиданием и дисперсией G2: ε i~N(0, G2).

Общий вид нормальной линейной модели парной регрессии в матричной форме:

Y= X* β+ ε ,

где

– случайный вектор-столбец значений результативной переменной размерности n x 1 ;

– матрица значений факторной переменной размерности n x 2 . Первый столбец является единичным, потому что в модели регрессии коэффициент β0 умножается на единицу;

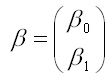
– вектор-столбец неизвестных коэффициентов модели регрессии размерности 2 x 1 ;

– случайный вектор-столбец ошибок модели регрессии размерности n x 1 .

Условия построения нормальной линейной модели парной регрессии, записанные в матричной форме:

1) факторная переменная xi – неслучайная или детерминированная величина, которая не зависит от распределения случайной ошибки модели регрессии β i;

2) математическое ожидание случайной ошибки модели регрессии равно нулю во всех наблюдениях:;

3) третье и четвёртое условия можно записать через ковариационную матрицы случайных ошибок нормальной линейной модели парной регрессии:

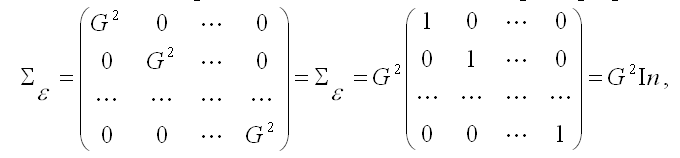
где G2 – дисперсия случайной ошибки модели регрессии ε;

In – единичная матрица размерности n x n.

Определение . Ковариацией называется показатель тесноты связи между переменными х и у , который рассчитывается по формуле:

где

– среднее арифметическое значение произведения факторного и результативного признаков;

Основными свойствами показателя ковариации являются:

а) ковариация переменной и константы равна нулю, т. е. cov(x,C)=0 (C=const);

б) ковариация переменной с самой собой равна дисперсии переменной, т. е. Cov(ε ,ε )=G2(ε ). По этой причине на диагонали ковариационной матрицы случайных ошибок нормальной линейной модели парной регрессии располагается дисперсия случайных ошибок;

4) случайная ошибка модели регрессии подчиняется нормальному закону распределения: εi~N(0, G2).