Коэффициенты эластичности

Коэффициенты эластичности наряду с индексами корреляции и детерминации для нелинейных форм связи применяются для характеристики зависимости между результативной переменной и факторными переменными. С помощью коэффициентов эластичности можно оценить степень зависимости между переменными х и у .

Коэффициент эластичности показывает, на сколько процентов изменится величина результативной переменной у , если величина факторной переменной изменится на 1 %.

В общем случае коэффициент эластичности рассчитывается по формуле:

где

– первая производная результативной переменной у по факторной переменной x .

Коэффициенты эластичности могут быть рассчитаны как средние и точечные коэффициенты.

Средний коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего среднего уровня

если факторная переменная х изменится на 1 % относительного своего среднего уровня

Общая формула для расчёта коэффициента эластичности для среднего значения

факторной переменной х :

где

– значение функции у при среднем значении факторной переменной х .

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

yi=β0+β1xi ,

средний коэффициент эластичности определяется по формуле:

Для полиномиальной функции второго порядка (параболической функции) вида:

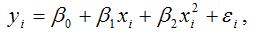
средний коэффициент эластичности определяется по формуле:

Для показательной функции вида:

средний коэффициент эластичности определяется по формуле:

Для степенной функции вида:

средний коэффициент эластичности определяется по формуле:

Это единственная нелинейная функция, для которой средний коэффициент эластичности

равен коэффициенту регрессии β1.

Точечные коэффициенты эластичности характеризуются тем, что эластичность функции зависит от заданного значения факторной переменной х1 .

Точечный коэффициент эластичности характеризует, на сколько процентов изменится результативная переменная у относительно своего значения в точке х1 , если факторная переменная изменится на 1 % относительно заданного уровня х1.

Общая формула для расчёта коэффициента эластичности для заданного значения х1 факторной переменной х :

Для каждой из разновидностей нелинейных функций средние коэффициенты эластичности рассчитываются по индивидуальным формулам.

Для линейной функции вида:

yi=β0+β1xi ,

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение линейной функции в точке х1 .

Для полиномиальной функции второго порядка (параболической функции) вида:

точечный коэффициент эластичности определяется по формуле:

В знаменателе данного показателя стоит значение параболической функции в точке х1 .

Для показательной функции вида:

точечный коэффициент эластичности определяется по формуле:

Для степенной функции вида:

точечный коэффициент эластичности определяется по формуле:

Докажем данное утверждение.

Запишем точечный коэффициент эластичности для степенной функции вида

через первую производную результативной переменной по заданной факторной переменной x 1:

Следовательно, Э(x1) = β1 , что и требовалось доказать.

Чаще всего коэффициенты эластичности применяются в анализе производственных функций. Однако их расчёт не всегда имеет смысл, потому что в некоторых случаях интерпретация факторных переменных в процентном отношении невозможна или бессмысленна.