
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод наименьших квадратов для двухфакторной производственной функции Кобба-Дугласа. Эффект от масштаба производства
Двухфакторную производственную функцию Кобба-Дугласа f(K,L) можно представить в виде:
Q=A*Ka*Lβ,
где Q – объём выпущенной продукции (в стоимостном или натуральном выражении);
K – объём основного капитала или основных фондов;
L – объём трудовых ресурсов или трудовых затрат (измеряемое количеством рабочих или количеством человеко-дней).
A,a,β – неизвестные числовые параметры производственной функции, которые подчиняются условиям:
1) 0≤а≤1;
2) 0≤β≤1;
3) A›0;
4) a+β=1.
Двухфакторная производственная функция Кобба-Дугласа относится к классу нелинейных по параметрам функций, которые можно свести к линейному виду.
Для того, чтобы привести двухфакторную производственную функцию Кобба-Дугласа к линейному виду, необходимо прологарифмировать обе части данной функции:
lnQj–lnLj=lna+β(lnKj–lnLj)+εj, ,
где εj – случайная ошибка производственной функции
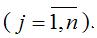
Для более наглядного представления данной модели регрессии воспользуемся методом замен:
yj= lnQj–lnLj;
b0=lna;
b1=β;
b=[ b0 b1]T;
xj= lnKj–lnLj;
δT(xj)=[0 xj].
В результате произведённых замен получим окончательный вид производственной функции Кобба-Дугласа, приведённой к линейной форме:
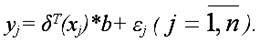
В данной функции неизвестным является только вектор коэффициентов b. Оценку данного вектора можно получить с помощью классического метода наименьших квадратов по формулам:
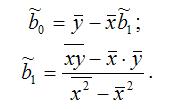
где

– среднее арифметическое значение переменной х :
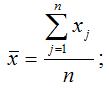

– среднее арифметическое значение переменной у :
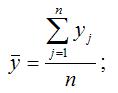
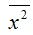
– среднее значение квадрата переменной х :

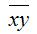
– среднее значение произведения переменных х и у :

После того, как будут получены МНК-оценки неизвестных коэффициентов b0 и b1 линеаризованной двухфакторной производственной функции Кобба-Дугласа, на их основе можно будет рассчитать оценки неизвестных параметров A,a,β исходной функции Кобба-Дугласа.
Эффектом от масштаба производства для двухфакторной производственной функции называется изменение объёма произведённой продукции при пропорциональном изменении затрат труда и капитала.
Пусть объём основного капитала изменился на величину nK , а объём трудовых затрат увеличился на величину nL . Рассчитаем величину изменения объёма производства для функции двухфакторной производственной Кобба-Дугласа:
Q(n)=A*(nKa)*(nLβ)= A*Ka*Lβ*na+β=Q*na+β.
Если справедливо неравенство (a+β)›1 , то функция Кобба-Дугласа имеет возрастающий эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q возрастает в na+β раз.
Если справедливо равенство (a+β)=1 , то функция Кобба-Дугласа имеет фиксированный эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q также возрастает в n раз.
Если справедливо неравенство (a+β)‹1 , то функция Кобба-Дугласа имеет убывающий эффект от масштабов производства, т. е. с увеличением факторных переменных K и L в n раз, объём производства Q возрастает меньшими чем n темпами.
Дата добавления: 2015-04-18; просмотров: 241; Мы поможем в написании вашей работы!; Нарушение авторских прав |