
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Метод максимума правдоподобия
Метод максимума правдоподобия (maximum likelihood function) применяется для определения неизвестных коэффициентов модели регрессии и является альтернативой методу наименьших квадратов. Суть данного метода состоит в максимизации функции правдоподобия или её логарифма.
Общий вид функции правдоподобия:

где

– это геометрическая сумма, означающая перемножение вероятностей по всем возможным случаям внутри скобок.
Предположим, что на основании полученных данных была построена модель регрессии бинарного выбора, где результативная переменная представлена с помощью латентной переменной:

Следовательно, вероятность события, что результативная переменная yi примет значение, равное единице, можно выразить следующим образом:

Вероятность события, что результативная переменная yi примет значение, равное нулю, можно выразить следующим образом:

В связи с тем, что для вероятностей считается справедливым равенство вида:
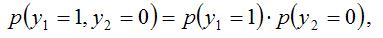
функция правдоподобия может быть записана как геометрическая сумма вероятностей наблюдений:

Для логит-регрессии и пробит-регрессии функция правдоподобия строится через сумму натуральных логарифмов правдоподобия следующим образом:

Оценки неизвестных параметров логит-регрессии и пробит-регрессии определяются с помощью максимизации функции правдоподобия:

Для определения максимума функции l(β,X ) необходимо вычислить частные производные этой функции по каждому из оцениваемых параметров и приравнять их к нулю. Результатом данной процедуры будет стационарная система уравнений:

С помощью преобразований данной системы уравнений переходим к системе нормальных уравнений, решениями которой и будут оценки максимального правдоподобия

Прежде, чем использовать пробит-регрессию и логит-регрессию для прогнозирования или анализа, необходимо проверить значимость вычисленных коэффициентов пробит и логит регрессий и моделей регрессии в целом. Подобная проверка осуществляется с помощью величины (l1-l0), где параметр l1 соответствует максимально правдоподобной оценке основной модели регрессии, а параметр l0 – оценка нулевой модели регрессии, т. е. yi=β0.
При проверке значимости коэффициентов пробит или логит-регрессии выдвигается основная гипотеза о незначимости данных коэффициентов:
H0:β1=β2=…=βk=0.
Тогда конкурирующей или альтернативной гипотезой будет гипотеза вида:
H1:β1≠β2≠…≠βk≠0.
Для проверки выдвинутых гипотез рассчитывается величина H=-2(l1–l0), которая распределена по χ2 закону распределения с k степенями свободы.
Критическое значение χ2 -критерия определяется по таблице по β2 распределения в зависимости от заданного значения вероятности а и степени свободы k .
При проверке гипотез возможны следующие ситуации:
Если величина H больше критического значение χ2-критерия, т.е.

то основная гипотеза отвергается, и коэффициенты модели регрессии являются значимыми. Следовательно, модель пробит или логит-регрессии также является значимой.
Если величина H меньше критического значение β2 -критерия, т. е.

то основная гипотеза принимается, и коэффициенты модели регрессии являются незначимыми. Следовательно, модель пробит или логит-регрессии также является незначимой.
Оценки неизвестных коэффициентов модели регрессии, полученные методом максимума правдоподобия, удовлетворяют следующему утверждению.
Пусть ω – это элемент, принадлежащий заданному пространству А . Если А является открытым интервалом, а функция L(ω) дифференцируема и достигает максимума в заданном интервале A , то оценки максимального правдоподобия удовлетворяют равенству вида:

Докажем данное утверждение на примере модели логит-регрессии.
Функция максимального правдоподобия для модели логит-регрессии имеет вид:

Продифференцируем полученную функцию по параметру β :

Следовательно, утверждение можно считать доказанным.
В том случае, если для модели регрессии справедливы предпосылки нормальной линейной модели регрессии, то оценки неизвестных коэффициентов, полученные с помощью метода наименьших квадратов, и оценки, полученные с помощью метода максимума правдоподобия, будут совпадать.
Дата добавления: 2015-04-18; просмотров: 246; Мы поможем в написании вашей работы!; Нарушение авторских прав |