
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нелинейный метод наименьших квадратов. Метод Койка
Если модель с распределенным лагом характеризуется бесконечной величиной максимального лага L, то для оценивания неизвестных параметров данной модели применяются нелинейный метод наименьших квадратов и метод Койка. При этом исходят из предположения о геометрической структуре лага, т. е. влияние лаговых значений факторной переменной на результативную переменную уменьшается с увеличением величины лага в геометрической прогрессии.
Если в модель включена только одна объясняющая переменная, то её можно представить в виде:

В модели с распределённым лагом (1) неизвестными являются три параметра: β0 , β 1 и λ . Найти оценки данных параметров с помощью традиционного метода наименьших квадратов невозможно по нескольким причинам, поэтому в данном случае используются нелинейный метод наименьших квадратов и метод Койка
Суть нелинейного метода наименьших квадратов заключается в том, что для параметра
λ определяются значения в интервале [-1;+1] с определённым шагом, например, 0,05 (чем меньше шаг, тем точнее будет результат).
Для каждого значения λ рассчитывается переменная z :
zt=xt+λxt–1+λ2xt–2+λ3xt–3+…+λLxt–L,
с таким значением лага L , при котором дальнейшие лаговые значения переменной x не оказывают существенного влияния на z .
На следующем этапе с помощью традиционного метода наименьших квадратов оценивается модель регрессии вида:
yt=β0+β1zt+εt (2)
и рассчитывается коэффициент детерминации R 2 . Данный процесс осуществляется для всех значений λ из интервала [-1;+1]. Оценками коэффициентов β0 , β1 и λ будут те, которые обеспечивают наибольшее значение R 2 для модели регрессии (2).
В основе метода или преобразования Койка лежит предположение о том, что если модель регрессия (1) справедлива для момента времени t , то она справедлива и для момента времени (t– 1):
yt–1=β0+β1xt–1+β1λxt–2+β1λ2xt–3+β1λ3xt–4+…+εt,
Умножим обе части данного уравнения на λ и вычтем их из модели регрессии (1). В результате получим выражение вида:
yt– λ yt–1= β0(1– λ)+β1xt+εt–λ εt–1 ,
или
yt= β0(1– λ)+β1xt+λyt–1 +νt, (2)
где νt= εt–λ εt –1 .
Полученная модель (2) является моделью авторегрессии, что позволяет проанализировать её краткосрочные и долгосрочные динамические свойства.
Значение переменной yt –1 в краткосрочном периоде (в текущем периоде) рассматривается как фиксированное, а воздействие переменной х на переменную у характеризует коэффициент β 1 .
Если xt в долгосрочном периоде (без учёта случайной компоненты модели) стремится к некоторому равновесному значению
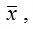
то yt и yt –1 также будут стремиться к своему равновесному значению, которое вычисляется по формуле:

из чего следует:

Долгосрочное влияние переменной х на переменную у характеризуется коэффициентом

Несмотря на то, что метод Койка очень удобен в вычислительном отношении (оценки параметров β0, β1 и λ можно рассчитать с помощью традиционного метода наименьших квадратов), оценки, полученные с его помощью, будут смещёнными и несостоятельными, т. к. нарушается первое условие нормальной линейной модели регрессии.
Дата добавления: 2015-04-18; просмотров: 376; Мы поможем в написании вашей работы!; Нарушение авторских прав |