Глоссарий. Автокорреляция уровней ряда – корреляционная зависимость между уровнями временного ряда.

Автокорреляция уровней ряда – корреляционная зависимость между уровнями временного ряда.

Аддитивная модель временного ряда – временной ряд представлен как сумма циклической, трендовой и случайной компонент.

Аналитический вид математической функции – основан на изучении математической природы связи исследуемых признаков.

Аналитическое выравнивание временного ряда – способ моделирования тенденции временного ряда посредством построения аналитической функции, характеризующей зависимость уровней ряда от времени.

Временной ряд – совокупность значений какого-либо показателя за несколько последовательных моментов времени.

Гипербола множественной регрессии -

Гомоскедастичность — дисперсия каждого отклонения -одинакова для всех значений х, в противном случае имеет место гетероскадастичность.

Графический вид математической функции - базируется на поле корреляции

Двухшаговый МНК:1)составляется приведенная форма модели и определяются численные значения параметров каждого ее уравнения обычным МНК, 2)выявляются эндогенные переменные, находящиеся в правой части структурного уравнения, параметры которого определяются двухшаговым МНК, и находятся расчетные значения по соответствующим уравнениям приведенной формы модели, 3)обычным МНК определяются параметры структурного уравнения, используя в качестве исходных данных фактические значения предопределенных переменных и расчетные значения эндогенных переменных, стоящих в правой части структурного уравнения

Дисперсионный анализ предшествует оценке значимости уравнения регрессии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части – «объясненную» и «остаточную».

Дисперсия на одну степень свободы (приведение дисперсий к сравниваемому виду): , ,

Достаточное условие идентификации – определитель матрицы, составленный из коэффициентов при переменных, отсутствующих в исследуемых уравнениях, не равен нулю, и ранг этой матрицы не менее числа эндогенных переменных системы без единицы.Для решения идентифицируемого уравнения применяется косвенный МНК, для решения сверхидентифицируемого – двухшаговый МНК.

Интеркорреляция – зависимость между объясняющими переменными, может привести к нежелательным последствиям – систем анормальных уравнений может оказаться плохо обусловленной и повлечь за собой неустойчивость и ненадежность оценок коэффициентов корреляции.

Коррелограмма – график зависимости значений автокорреляционной функции временного ряда от величины лага.

Косвенный МНК: 1)составляется приведенная форма модели и определяются численные значения параметров каждого ее уравнения обычным МНК, 2)путем алгебраических преобразований делается переход от приведенной формы к уравнениям структурной формы модели, получая тем самым численные оценки структурных параметров.

Коэффициент детерминации - показывает качество подбора функции и характеризует долю дисперсии результативного признака, объясняемую регрессией, в общей дисперсии результативного признака.

Коэффициент регрессии b – показывает среднее изменение результата с изменением фактора на одну единицу.

Коэффициент эластичности - показывает силу связи между переменными и является относительным показателем силы связи, поскольку выражен в процентах:

Критерий F - характеризует сопоставление факторной и остаточной дисперсии в расчете на одну степень свободы: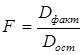

Лаг – число периодов, по которым рассчитывается коэффициент корреляции временного ряда.

Линейная функция множественной регрессии -

Линейный коэффициент корреляции – показывает тесноту связи между признака и изменяется в пределах от -1 до 1. Чем ближе коэффициент корреляции по модулю к единице, тем теснее связь. Определяется по формуле

Метод наименьших квадратов для линейной парной регрессионной модели – параметры а и b находятся из систему уравнений . МНК позволяет получить такие оценки параметров а и b при которых сумма квадратов отклонений фактических значений результативного признака от расчетных минимальна.

МНК для оценки параметров множественной линейной регрессии - для уравнения 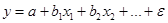система нормальных уравнений составит: , ее решением может быть осуществлено методом определителей

Множественная корреляция -практическая значимость уравнения множественной регрессии оценивается с помощью показателя множественной корреляции и его квадрата – коэффициента детерминации:

Множественная регрессия широко используется в решении проблем спроса доходности акций, при изучении функций издержек производства, в макроэкономический расчетах и целого ряда других вопросов эконометрики. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное воздействие их на моделируемый показатель.

Модель временных рядов представляет собой зависимость результативного признака от переменной времени

Мультиколлинеарность факторов - более чем два фактора связаны между собой в линейной зависимости, то есть имеет место совокупное воздействие факторов друг на друга. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью МНК.

Мультипликативная модель временного ряда – временной ряд представлен как произведение циклической, трендовой и случайной компонент.

Необходимое условие идентификации- выполнение счетного правила:D+1=H – уравнение идентифицируемо, D+1<H – уравнение неидентифицируемо, D+1>H – уравнение сверхидентифицируемо (Н – число эндогенных переменных в уравнении, D – число предопределенных переменных, отсутствующих в уравнении, но присутствующих в системе)

Общая сумма квадратов отклонений

Остаточная сумма квадратов:

Парная регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной у рассматривается как функция одной независимой (объясняющей) переменной х, то есть это модель вида:

Предопределенные переменные– экзогенные и лаговые (за предыдущие моменты времени) эндогенные переменные системы.

Приведенная форма модели - система линейных функций эндогенных переменных от всех предопределенных переменных системы :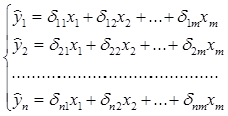

Регрессионные модели с одним уравнением – зависимая переменная представляется в виде функции

Система взаимосвязных (совместных) уравнений – одни и те же зависимые переменные в одних уравнениях входят в левую часть, а в других – в правую

Система независимых уравнений – каждая зависимая переменная у рассматривается как функция одного и того же набора факторов х:

Система рекурсивных уравнений – зависимая переменная у одного уравнения выступает в виде фактора х в другом уравнении: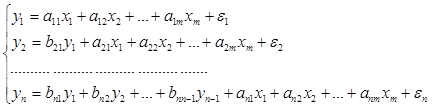

Системы одновременных уравнений описываются системами взаимозависимых регрессионных уравнений

Совмещенные уравнения регрессии - к уравнениям, которые отражают не только влияние факторов, но и их взаимодействие, так если , то можно построить совмещенное уравнение:

Спецификация модели парной регрессии включает в себя следующие этапы:1) выделение факторов, наиболее существенно влияющих на результативный признак; 2)уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь по совокупности наблюдений. Практически в каждом отдельном случае величина у складывается из двух слагаемых: теоретического значения результативного признака и случайной величины, характеризующей отклонения реального значения результативного признака от теоретического – ;3)возмущение обусловлено тремя источниками: спецификацией модели, выборочным характером и особенностями измерения переменных. Каждый из данных источников может стать причиной ошибок, вследствие которых могут быть получены неверные выводы; 4)выбор вида математической функции; 5) построение графика линейной регрессии. Линейная регрессия сводится к нахождению уравнения вида: или

Стандартная ошибка коэффициента корреляции 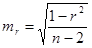, фактическое значение величины t – критерия Стьюдента определяется как

Стандартная ошибка коэффициента регрессии рассчитывается по формуле: , фактическое значение t-критерия Стьюдента 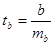, которое сравнивается с табличным значением при определенном уровне значимости и числе степеней свободы (n-2). Доверительный интервал для коэффициента регрессии определяется как

Стандартная ошибка параметра а определяется по формуле: , t-критерий: , его величина сравнивается с табличным значением при числе степеней свободы

Степенная функция множественной регрессии -

Степень свободы – число возможных направлений варьирования признака. Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов: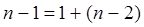

Сумма квадратов отклонений, обусловленных регрессией:

Условие включения независимых переменных в уравнение множественной регрессии: матрица парных коэффициентов между ними была бы единичной, и мела бы определитель, равный единице:

Фиктивные переменные – переменные, полученные путем перевода качественных признаков переменных в количественных, то есть при присвоении цифровых меток.

Частные коэффициенты эластичностипозволяют определить эффекты влияния других факторов присоединены в них к свободному члену уравнения множественной регрессии

Частные уравнения линейного уравнения множественной регрессии - уравнения регрессии, которые имеют следующий вид: , , …………………………………………., . При подстановке в эти уравнения средних значений соответствующих факторов они принимают вид парной регрессии: ,где: , , ………………………………………….,

Экзогенные переменные – независимые переменные, которые определяются вне системы х.

Эконометрика – это наука об измерении и анализе экономических явлений и их взаимосвязей. Зарождение эконометрики является следствием междисциплинарного подхода к изучение экономики. Эта наука возникла в результате взаимодействия и объединения трех компонентов: экономической теории, статистических и математических методов. Впоследствии к ним присоединилась вычислительная техника как условие развития эконометрики.

Экспериментальныйвид математической функции– показывает статистику явлений.

Экспоненциальная функция множественной регрессии -

Эндогенные переменные – взамосвязные переменные которые определяются внутри модели у.

Этапы эконометрического исследования: 1)постановка проблемы, 2)получение данных, анализ их качества, 3)спецификация модели, 4)оценка параметров, 5)интерпретация результатов