Гидродинам подобие. Число Рейнольдса

Посмотрим, какому условию должны удовлетворять те же геометрически и кинематически подобные потоки для того, чтобы было обеспечено их гидродинамическое подобие при наличии сил вязкости, а, следовательно, и потерь энергии, т.е. при каком условии числа Eu будут одинаковыми для этих потоков.

Уравнение Бернулли для этого случая примет вид:

,

или по аналогии с предыдущими рассуждениями, учтя, что , можно написать

Как видно из последнего уравнения, числа Eu будут иметь одинаковые значения для рассматриваемых потоков, а сами потоки будут подобны друг другу гидродинамически при условии равенства коэффициентов сопротивления (равенство коэффициентов и для сходственных сечений двух потоков следует из их кинематического подобия). Таким образом, коэффициенты сопротивлений в подобных потоках должны быть одинаковыми, а это значит, что потери напора для сходственных участков пропорциональны скоростным напорам.

Рассмотрим очень важный в гидравлике случай движения жидкости - движение с трением в цилиндрической трубе, для которого коэффициент трения можно описать формулой .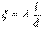

Для геометрически подобных потоков отношение 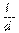одинаково, следовательно, условием гидродинамического подобия в данном случае является одинаковое значение для этих потоков коэффициента . Он выражается через напряжение трения 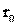на стенке и динамическое давление, как было установлено ранее, следующим образом: .

Следовательно, для двух подобных потоков I и IIможно записать ,

т. е. напряжения трения пропорциональны динамическим давлениям.

Учитывая закон трения Ньютона и тот факт, что в последних уравнениях 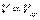, предыдущие отношения, равные k, можно выразить

где индекс у = 0 означает, что производная взята при у = 0, т. е. у стенки трубы. При этом заметим, что закон трения Ньютона применим лишь при ламинарном течении. Однако, как было показано выше, при турбулентном течении в трубах вблизи стенок образуется тонкий ламинарный слой, внутри которого справедлив закон трения Ньютона. Поэтому напряжение трения на стенке может определяться по этому закону также и при турбулентном течении.

После умножения и деления на диаметр трубы d и перегруппировки множителей получим:

.

Здесь буквой С обозначено выражение в квадратных скобках, представляющее собой безразмерный градиент скорости вблизи стенки.

Для кинематически подобных потоков величина C одинакова, поэтому после сокращения на С условие динамического подобия потоков перепишем в виде

.

или, переходя к обратным величинам

.

В этом заключается критерий подобия Рейнольдса, который можно сформулировать следующим образом: для гидродинамического подобия геометрически и кинематически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.