Сила давления жидкости на криволинейные поверхности

Выделим на некоторой цилиндрической поверхности АВ (рис. 9) элементарную площадку с центром тяжести, погруженным на глуби­ну h под свободную поверхность жидкости. Если давление на по­верхности жидкости равно р₀, то гидростатическое (абсолютное) давление в центре тяжести площадки составит

р=р_{0 +} .

Тогда dР − элементарная сила абсолютного гидростатического давления на площадку будет равна

dP = (p₀ + ) (2.33)

и направлена по нормали к ней, проведенной через центр тяжести.

Рис.9

Разложим элементарную силу абсолютного гидростатического давления на вертикальную и горизонтальную составляющие, обозна­чив угол между элементарной силой dP и вертикалью через :

(2.34)

где ·cos = _xoy − площадь проекции на плоскость XOY; ·sin = _zoy − площадь проекции на плоскость ZOY.

С учетом приведенных выше равенств уравнение (2.34) можно записать в виде:

(2.35)

Если всю поверхность АВ разбить на ряд элементарных площа­док и для каждой из них определить значения dP_В и dP_Г, то вертикальную Р_В и горизонтальную Р_Г составляющие силы абсолютного гидростатического давления жидкости Р на цилиндрическую поверхность АВ можно найти суммированием всех элементарных сил dP_В и dP_Г или интегрированием уравнений (2.35):

(2.36)

. (2.37)

Первые интегралы в уравнениях (2.36) и (2.37) равны соответственно площадям проекций цилиндрической поверхности АВ на горизонтальную XOY и вертикальную ZOY плоскости, т.е.

, а .

Проведя вертикальные образующие через различные точки пара­метра элементарной площадки до координатной плоскости XOY, получим некоторый элементарный объем abcd, равный h· _xoy, т.е. объем, записанный под вторым интегралом в уравнении (2.36).Это уравнение теперь можно записать в виде

Р_В=р₀ + (объем ABCД). (2.38)

Следовательно, вертикальная составляющая силы абсолютного гидростатического давления равна сумме силы внешнего давления на горизонтальную проекцию цилиндрической поверхности АВ (пе­редающегося от воздействия внешней силы на поверхность жидкости) и веса жидкости в объеме АВСД, ограниченном цилиндрической по­верхностью АВ, вертикальными плоскостями АД и ВС свободной по­верхности жидкости, а также передней и задней вертикальными плоскостями.

Второй интеграл уравнения (2.37) равен статическому моменту площади проекции цилиндрической поверхности АВ на вертикальную плоскость ZOY относительно оси OY:

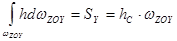, (2.39)

где h_с − глубина погружения центра тяжести площади .

Из уравнений (2.37) и (2.39) находим

P_Г =(p₀+ _c)· . (2.40)

Это уравнение идентично уравнению (2.25). Следовательно, го­ризонтальная составляющая силы полного гидростатического давле­ния на цилиндрическую поверхность АВ равна силе абсолютного гидростатического давления, под воздействием которого находится вертикальная плоская стенка, равная по площади вертикальной про­екции цилиндрической поверхности АВ.

Складывая составляющие силы давления Р_В и Р_Г по правилу параллелограмма, получаем силу абсолютного гидростатического давления Р, действующую на цилиндрическую поверхность АВ:

. (2.41)

Построим эпюру абсолютного гидростатического давления на криволинейную поверхность АВ. Объем АВС₁Д₁ является эпюрой вертикальной составляющей абсолютного гидростатического давления на рассматриваемую поверхность АВ (рис. 10).

Рис.10

Эту эпюру можно рассматривать как состоящую из двух частей: эпюры АВСД, изобретающей избыточное (весовое) давление на площадь проекции поверхности АВ на плоскость XOY, и эпюры ДСС₁Д₁, характеризующей внешнее давление р₀. Сила давления Р_В, равная численно объему АВС₁Д₁, проходит через центр тяжести этого объема.

Эпюра горизонтальной составляющей абсолютного гидростатического давления на криволинейную поверхность АВ строится так же, как и для плоских стенок. В данном случае она представляется фигурой KZMN, которую можно рассматривать как состоящую из двух частей: эпюры KZM₁N₁, изображающей избыточное (весовое) давление жидкости, и эпюры MNN₁M₁, характеризующей внешнее давление р₀. Сила давления Р_T, равная объему эпюры KZM₁N₁, проходит через центр тяжести этого объема.

7. Закон Паскаля: формула и применение

Если мы положим на стол тяжелую стопку книг, то мы увеличим давление не только на стол, но и соответственно, на пол под столом. Стены, потолок, окна и двери этого давления на себе не почувствуют. Даже если мы сложим на стол всю одежду из шкафов, еду из холодильника, телевизор, гантели и вдобавок взгромоздимся с ногами сами, стены и потолок не ощутят никаких изменений. Разве что их может задеть щепкой от разлетевшегося под весом всего этого добра стола, но изменения в давлении на них будут равны нулю. С газами и жидкостями дело обстоит иначе. Если в закрытом сосуде мы изменим давление на наполняющую сосуд жидкость или газ, то изменение в давлении ощутят на себе абсолютно все стенки этого сосуда. Можно самостоятельно проделать опыт, наглядно подтверждающий это явление. Для этого необходимо взять плотный резиновый шарик и наполнить его водой, а потом завязать или закупорить как-то иначе. Аккуратно, чтобы не порвать, проделываем иголкой несколько дырок в разных местах наполненного водой шарика. Сквозь дырки начинает сочиться вода. А теперь, если мы сожмем шар в руках, мы увидим, что вода начинает выливаться гораздо активнее абсолютно через все отверстия. То есть, увеличив давление в местах сжатия, мы видим, что давление увеличилось также одинаково во всех направлениях, на все стенки сосуда, то есть, в данном случае, шарика.

То же самое будет, если наполнить шарик дымом. Это происходит вследствие того, что активно перемещающиеся частицы жидкости и газа перемешиваются по всему объему, и давление, уменьшившее объем для их свободного перемещения в одном месте, вызовет такое же уменьшение объема по всем направлениям. В этом и состоит закон Паскаля: жидкости и газы передают оказываемое на них давление по всем направлениям одинаково. Закон этот был открыт в 17 веке французским ученым Паскалем и потому носит его имя.

Закон Паскаля описывается формулой давления:

p=F/S,

где p – это давление,
F – приложенная сила,
S – площадь сосуда.

Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться. Измеряется давление в ньютонах на метр квадратный или в паскалях (Па), в честь ученого, открывшего закон Паскаля. Его применение лежит в основе многих устройств и довольно распространено в производстве. Это, в частности, гидравлические прессы, пневматические тормоза и инструменты и многое другое.