
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Вопрос № 38. Основное уравнение работы центробежных насосов.
Основное уравнение центробежного насоса впервые в самом общем виде было получено в 1754 г. Л. Эйлером и носит ею имя.
Рассматривая движение жидкости внутри рабочего колеса, сделаем следующие допущения: насос перекачивает идеальную жидкость в виде струй, т. е. в насосе отсутствуют все виды потерь энергии. Число одинаковых лопастей насоса бесконечно большое (z = µ), толщина их равна нулю (d= 0), а угловая скорость вращения колеса постоянна (w= const.).
К рабочему колесу центробежного насоса со скоростью Vo жидкость подводится аксиально, т. е. в направлении оси вала. Затем направление струй жидкости изменяется от осевого до радиального, перпендикулярного оси вала, а скорость благодаря центробежной силе увеличивается от значения V1 в пространстве между лопастями рабочего колеса до значения V2 на выходе из колеса.
В межлопастном пространстве рабочего колеса при движении жидкости различают абсолютную и относительную скорости потока. Относительная скорость потока — скорость относительно рабочего колеса, а абсолютная — относительно корпуса насоса.


Рис. Схема движения жидкости в рабочем колесе центробежного насоса
Абсолютная скорость равна геометрической сумме относительной скорости жидкости и окружной скорости рабочего колеса. Окружная скорость жидкости, выходящей между лопастями рабочего колеса, совпадает с окружной скоростью колеса в данной точке.
Окружная скорость жидкости (м/с) на входе в рабочее колесо

Окружная скорость жидкости на выходе из рабочего колеса (м/с)
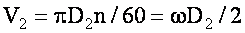
где n—частота вращения рабочего колеса, об/мин; D1 и D2 — внутренний и внешний диаметры рабочего колеса, м, w— угловая скорость вращения рабочего колеса рад/с
При движении рабочего колеса частицы жидкости движутся вдоль лопастей. Вращаясь вместе с рабочим колесом, они приобретают окружную скорость, а перемещаясь вдоль лопастей — относительную.
Абсолютная скорость v движения жидкости равна геометрической сумме ее составляющих: относительной скорости wи окружной u, т. е. v = w + и.
Связь между скоростями частиц жидкости выражается параллелограммом или треугольниками скоростей, что позволяет дать понятие о радиальной и окружной составляющих абсолютной скорости.
Радиальная составляющая

окружная составляющая

где a— угол между абсолютной и окружной скоростями (на входе рабочего колеса a1 и на выходе a2).
Угол b между относительной и окружной скоростями характеризует очертание лопастей насоса .
Исследуем изменение за 1 с момента количества движения Массы жидкости т = rQ, где r — плотность жидкости; Q— подача насоса.
Используя теорему механики об изменении моментов количества движения применительно к движению жидкости в канале рабочего колеса, выведем основное уравнение центробежного насоса, которое позволит определить развиваемый насосом напор (или давление). Эта теорема гласит: изменение во времени главного момента количества движения системы материальных точек относительно некоторой оси равно сумме моментов всех сил, действующих на эту систему.
Момент количества движения жидкости относительно оси рабочего колеса во входном сечении

Момент количества движения на выходе из рабочего колеси

где r1 и r2 — расстояния от оси колеса до векторов входной V1 и выходной V2 скоростей соответственно.
Согласно определению момента системы можно записать:

Так как в соответствии с рис

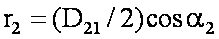

Группы внешних сил — силы тяжести, силы давления в расчетных сечениях (входа-выхода) и со стороны рабочего колеса и силы трения жидкости на обтекаемых поверхностях лопастей рабочего колеса — действуют на массу жидкости, заполняющей межлопастные каналы рабочего колеса.
Момент сил тяжести относительно оси вращения всегда равен нулю, так как плечо этих сил равно нулю. Момент сил давления в расчетных сечениях по этой же причине также равен нулю. Если силами трения пренебрегают, то и момент сил трения равен нулю. Тогда момент всех внешних сил относительно оси вращения колеса сводится к моменту Мк динамического воздействия рабочего колеса на протекающую через него жидкость, т. е.

Произведение Мк на относительную скорость равно произведению расхода на теоретическое давление PT,создаваемое насосом, т. е. равно мощности, передаваемой жидкости рабочим колесом. Следовательно,

Это уравнение можно представить в виде

Разделив обе его части на Q, получим

Учитывая, что напор Н = Р/(pg) и подставив это значение получим

Если пренебречь силами трения, то можно получить зависимости, называемые основными уравнениями лопастного насоса. Эти уравнения отражают зависимость теоретического давления или напора от основных параметров рабочего колеса. Переносные скорости на входе в осевой насос и на выходе из него |одинаковы, поэтому уравнение принимает вид

В большинстве насосов жидкость в рабочее колесо поступает практически радиально и, следовательно, скорость V1 » 0. C учетом вышеизложенного
 или
или 
Теоретические давление и напор, развиваемые насосом, тем больше, чем больше окружная скорость на внешней окружности рабочего колеса, т. е. чем больше его диаметр, частота вращения и угол b2 , т. е. чем «круче» расположены лопатки рабочего колеса.
Действительные давление и напор, развиваемые насосом, меньше теоретических, так как реальные условия работы насоса отличаются от идеальных, принятых при выводе уравнения. Давление, развиваемое насосом, уменьшается главным образом из-за того, что при конечном числе лопастей рабочего колеса не все частицы жидкости отклоняются равномерно, вследствие чего уменьшается абсолютная скорость. Кроме того, часть энергии расходуется на преодоление гидравлических сопротивлении. Влияние конечного числа лопастей учитывают введением поправочного коэффициента k(характеризующею уменьшение окружной составляющей скорости V2u), уменьшение давления вследствие гидравлических потерь — введением гидравлического коэффициента полезного действия hr . С учетом этих поправок полное давление

а полный напор 
Значение коэффициента hr зависит от конструкции насоса, его размеров и качества выполнения внутренних поверхностей проточной части колеса. Обычно значение hr составляет 0,8...0,95. Значение k при числе лопастей от 6 до 10, a2 = 8...140 и V2u = 1,5...4 м/с колеблется от 0,75 до 0,9.
При вращении рабочего колеса центробежного насоса жидкость, находящаяся между лопатками, благодаря развиваемой центробежной силе выбрасывается через спиральную камеру в напорный трубопровод. Уходящая жидкость освобождает занимаемое ею пространство в каналах на внутренней окружности рабочего колеса, поэтому у входа в рабочее колесо образуется вакуум, а на периферии — избыточное давление. Под действием разности атмосферного давления в приемном резервуаре и пониженного давления на входе в рабочее колесо жидкость по всасывающему водопроводу поступает в межлопаточные каналы рабочего колеса.
Центробежный насос может работать только в том случае, когда его внутренняя полость заполнена перекачиваемой жидкостью не ниже оси насоса, поэтому насосную установку оборудуют устройством для залива насоса.
Вопрос №39. Рабочая характеристика центробежного насоса Н-0.
Характеристикой центробежного насоса, или внешними и рабочими характеристиками, называют графическую зависимость основных показателей насоса, таких как напор, мощность и КПД, от подачи, а кавитационной характеристикой — график зависимости напора, подачи и КПД от избыточного напора на всасывании Н.
Все параметры насоса взаимосвязаны, и изменение одного из них неизбежно влечет за собой изменение других. Если при постоянной частоте вращения ротора увеличить подачу насоса, то создаваемый им напор уменьшится. При изменении условий работы КПД насоса также меняется: при некоторых определенных значениях расхода и напора КПД насоса будет максимальным, а при всех других режимах его работы насос работает с худшим КПД. Отметим, что на КПД сильно влияет коэффициент быстроходности .
Характеристики центробежных насосов наглядно показывают эффективность их работы на различных режимах и позволяют точно подобрать наиболее экономичный насос для заданных условий работы.
Рабочая характеристика насоса вследствие гидравлических потерь и непостоянства гидравлического КПД отличается от теоретической.
Потери напора в рабочем колесе складываются из потерь на Трение в каналах колеса, потерь на удар при отклонениях скорости на входе в колесо от касательного направления в лопатке и др.
Как видно из рис. б, все зависимости строят на одном графике в соответствующих масштабах, причем подачу Q насоса откладывают по оси абсцисс, а напор Н, вакуумметрическую высоту, мощность и КПД — по оси ординат.
Чтобы определить по рабочей характеристике необходимые параметры насоса, поступают следующим образом. По заданной подаче насосаQoнаходят на кривой Q —Н точку С, от которой проводят горизонтальную линию до пересечения со шкалой Н, где находят напор, соответствующий заданному расходу. Для определения мощности и КПД насоса проводят горизонтальные прямые из точек А и В и на шкалах N и h и таким образом находят соответствующие значения Noиho.
Рабочие характеристики насосов имеют несколько отличительных точек и областей. Начальная точка характеристики соответствует нулевой подаче насоса Q=0, что наблюдается при работе насоса с закрытой задвижкой на напорном трубопроводе. Как видно из рис. а, центробежный насос в этом случае развивает некоторый напор и потребляет мощность, которая расходуется на механические потери и нагрев воды в насосе.

Режим работы насоса, соответствующий максимальному КПД, называют оптимальным. Главная цель подбора насосов — обеспечение их эксплуатации при оптимальном режиме, учитывая, что кривая КПД имеет в зоне оптимальной точки пологий характер, однако на практике пользуются рабочей частью характеристики насоса (зона, соответствующая примерно 0,9hмакс, в пределах которой допускаются подбор и эксплуатация насосов).
Кавитационные характеристики необходимы для оценки кавитационных свойств насосов и правильного выбора высоты всасывания. Для построения кавитационной характеристики насоса его подвергают кавитационным испытаниям на специальных стендах.
В определенных границах изменения избыточного напора на всасывании Hвс.изб значения Q, Н и hостаются неизменными. При некоторых значениях Нвс.изб появляются шумы и треск при работе насоса, характеризующие наступление местной кавитации. При дальнейшем понижении Нвс.избзначенияQ, Н и h начинают постепенно уменьшаться, кавитационный шум усиливается и в конечном счете происходит срыв работы насоса. Точно установить момент начала воздействия кавитации на Q, Н и h не представляется возможным, поэтому условно принимают за минимальную избыточную высоту всасывания Нвс.избmin, то ее значение, при котором подача насоса падает на 1 % своего первоначального значения.
Очень часто на рабочие характеристики насосов наносят еще кривую Нвак — Q, которая дает значения допустимой вакуумметрической высоты всасывания в зависимости от подачи насоса.
Вопрос № 40. Треугольники скоростей. Пересчет и моделирование параметров.
В центробежном насосе передача энергии осуществляется за счет силового взаимодействия лопастного аппарата рабочего колеса с жидкостью.
Рис.2.1. Движение жидкости в рабочем колесе В межлопаточных каналах рабочего колеса частицы жидкости участвуют в сложном движении: · переносном - вместе с рабочим колесом; · относительном - по отношению к стенкам межлопаточных каналов; · абсолютном - результирующем по отношению к вышеназванным движениям. Вектор абсолютной скорости частицы Относительная скорость частицы где i=1,2. Индекс "1" - соответствует параметрам жидкости на входе в рабочее колесо, а "2" - на выходе из него. | |
| 2.1. Основное уравнение турбомашин | |
| (турбинное уравнение Эйлера) | |
Основное уравнение турбомашин связывает геометрические и кинематические характеристики рабочего колеса с развиваемым им напором. При его выводе принимают, что траектория частиц жидкости в межлопаточных каналах повторяет очертания профиля лопасти, т.е. для рабочего колеса делается допущение о бесконечности числа расположенных на нем бесконечно тонких лопаток (признаком этого будет служить символ ¥ в качестве индекса).
Вывод основан на уравнении моментов количества движения при установившемся движении жидкости в равномерно вращающихся каналах, согласно которому изменение в единицу времени момента количества движения жидкости L, находящейся в канале, равно моменту действующих на нее внешних сил:
 К внешним силам, действующим на жидкость в канале, относят силы, с которыми стенки канала действуют на жидкость, силы давления, силы трения, силы тяжести. Анализ показывает, что равнодействующие сил давления на внутренней и внешней образующих колеса проходят через ось вращения и момента не создают. Силы тяжести из-за симметрии рабочего колеса уравновешаны, а силы трения, действующие по периферийным поверхностям вращения малы. На основании вышеперечисленного предполагают, что момент создают только силы, возникающие от взаимодействия стенок рабочих каналов с жидкостью, находящейся в них.
Этот момент внешних сил связан с гидравлической мощностью насоса Nг и угловой скоростью вращения w следующим соотношением:
К внешним силам, действующим на жидкость в канале, относят силы, с которыми стенки канала действуют на жидкость, силы давления, силы трения, силы тяжести. Анализ показывает, что равнодействующие сил давления на внутренней и внешней образующих колеса проходят через ось вращения и момента не создают. Силы тяжести из-за симметрии рабочего колеса уравновешаны, а силы трения, действующие по периферийным поверхностям вращения малы. На основании вышеперечисленного предполагают, что момент создают только силы, возникающие от взаимодействия стенок рабочих каналов с жидкостью, находящейся в них.
Этот момент внешних сил связан с гидравлической мощностью насоса Nг и угловой скоростью вращения w следующим соотношением:
 Подставляя найденные величины в закон изменения момента количества движения во времени получим уравнение Эйлера:
Подставляя найденные величины в закон изменения момента количества движения во времени получим уравнение Эйлера:
 или
или
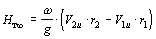 . (2.1)
Уравнение Эйлера связывает теоретический напор насоса со скоростями движения жидкости, которые зависят от подачи насоса, угловой скорости вращения рабочего колеса, а также с его геометрическими характеристиками.
Поток на входе в рабочее колесо создается предшествующим ему устройством (подводом). Следовательно момент скорости (закрутка) . (2.1)
Уравнение Эйлера связывает теоретический напор насоса со скоростями движения жидкости, которые зависят от подачи насоса, угловой скорости вращения рабочего колеса, а также с его геометрическими характеристиками.
Поток на входе в рабочее колесо создается предшествующим ему устройством (подводом). Следовательно момент скорости (закрутка)  определяется конструкцией подвода. Подводящие устройства многих насосов не закручивают поток и момент скорости на входе равен нулю. В этом случае теоретический напор определится по следующему уравнению: определяется конструкцией подвода. Подводящие устройства многих насосов не закручивают поток и момент скорости на входе равен нулю. В этом случае теоретический напор определится по следующему уравнению:
 где
где  - окружная скорость на периферии колеса.
Учитывая, что - окружная скорость на периферии колеса.
Учитывая, что
 ,
где n - частота вращения, об/мин;
а проекция абсолютной скорости на выходе из колеса на окружную скорость, как следует из треугольника скоростей (см. рис. 2.1), определяется выражением ,
где n - частота вращения, об/мин;
а проекция абсолютной скорости на выходе из колеса на окружную скорость, как следует из треугольника скоростей (см. рис. 2.1), определяется выражением
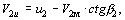 уравнение для теоретического напора примет вид:
уравнение для теоретического напора примет вид:

Это уравнение показывает, что напор зависит от величины меридианной составляющей абсолютной скорости на выходе из колеса, которая связана с подачей насоса уравнением где b2 - ширина канала рабочего колеса на выходе. Теоретический напор при конечном числе лопастей Hт меньше Из рассмотрения треугольников скоростей (рис.2.1), на основании теоремы косинусов можно записать откуда С учетом приведенных зависимостей уравнение Эйлера может быть преобразовано к виду: где Величину С целью уменьшения потерь в насосе желательно, чтобы статическая часть напора преобладала, причем за счет центробежной составляющей. |
Вопрос №41. Работа центробежного насоса на данный трубопровод.
Совокупность насоса, приемного и напорного резервуаров, трубопроводов, связывающих вышеперечисленные элементы, регулирующей и запорной арматуры, а также контрольно-измерительной аппаратуры составляет насосную установку. Для перемещения жидкости по трубопроводам из приемного резервуара в напорный необходимо затрачивать энергию на:
· подъем жидкости на высоту Hг, равную разности уровней в резервуарах (эту величину называют геометрическим напором насосной установки);
· преодоление разности давлений в них pпи pн;
· преодоление суммарных гидравлических потерь Shп во всасывающем и напорном трубопроводах.
Таким образом, энергия, необходимая для перемещения единицы веса жидкости из приемного резервуара в напорный по трубопроводам, или потребный напор установки определяется по выражению:

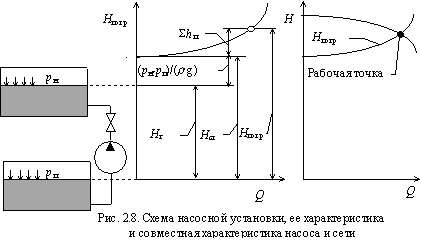
Характеристикой насосной установки называют зависимость потребного напора от расхода жидкости. Геометрический напор Hг, давления pпи pн от расхода не зависят. Гидравлические потери являются функцией расхода и зависят от режима движения. При ламинарном режиме характеристика трубопровода изображается прямой линией, при турбулентном движении в шероховатых трубах потери напора, а следовательно и характеристика имеет вид параболы.
|
На рис.2.8 приведена схема насосной установки и ее характеристика. Насос работает на таком режиме, при котором потребный напор равен напору насоса. Для определения режима работы насоса необходимо на одном и том же графике в одинаковых масштабах нанести характеристику насоса и насосной установки. Точка пересечения характеристик называетсярабочей точкой.
Дата добавления: 2015-04-18; просмотров: 2042; Мы поможем в написании вашей работы!; Нарушение авторских прав |

 может быть представлен суммой переносной (окружной) скорости
может быть представлен суммой переносной (окружной) скорости  и относительной скорости
и относительной скорости  .
.


 (2.2)
(2.2)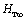 , что учитывается введением в уравнение Эйлера поправочного коэффициента e
, что учитывается введением в уравнение Эйлера поправочного коэффициента e .
.


 - напор, создаваемый за счет действия центробежных сил в потоке;
- напор, создаваемый за счет действия центробежных сил в потоке; - напор, создаваемый за счет изменения относительной скорости в канале рабочего колеса;
- напор, создаваемый за счет изменения относительной скорости в канале рабочего колеса; - напор, создаваемый за счет изменения абсолютной скорости в канале рабочего колеса.
- напор, создаваемый за счет изменения абсолютной скорости в канале рабочего колеса.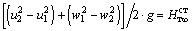 - называют статической частью напора, а
- называют статической частью напора, а  - динамической частью напора.
- динамической частью напора.