Понятие о гидравлически гладких и шероховатых трубах.

А) трубы гидравлически гладкие.

Б) Вихри создают дополнительное сопротивление -> трубы гидравлически шероховатые.

Характеризует шероховатость безразмерной величиной

- абсолютная шероховатость

r – радиус трубы

– относительная шероховатость

- относительная гладкость

Эквивалентная шероховатость – такая шероховатость, при которой потери напора в трубе получаются такими же, как и при фактической неоднородной шероховатости. Значение приводится в справочниках.

37. Коэффициенты λ и С. Законы гидравлического сопротивления.

Для гидравлически гладких труб:

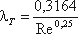формула Голазиуса при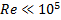

формула Конакова до Re=6*10⁵

Для шероховатых труб:

Формула Никурадзе

универсальная формула А.Д. Альтшуля:

где Δ_э - эквивалентная абсолютная шероховатость.

Формула Шифренсона (упрощенная формула Альтшуля):

Если 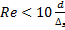ф. Голазиуса.

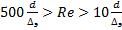ф. Альтшуля.

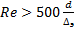ф. Шифренсона

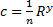- формула Павловского

n – коэффициент шероховатости. Зависит от материала или составления труб (табличные данные)

R – гидравлический радиус

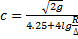- формула Зегжда

Рис. 4.7. График Никурадзе

Прямая I соответствует ламинарному режиму движения жидкости.

Далее на графике можно рассматривать три области.

Первая область - область малых Re и Δ/r₀, где коэффициент λ не зависит от шероховатости, а определяется лишь числом Re (отмечена на рис.4.7 прямой II ). Это область гидравлически гладких труб. Если число Рейнольдса лежит в диапазоне 4000 < Re < 10(d / Δ _э) коэффициент λ определяется по полуэмпирической формуле Блазиуса

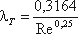
Для определения существует также эмпирическая формула П.К. Конакова, которая применима для гидравлически гладких труб

Во второй области, расположенной между линий II и пунктирной линией справа, коэффициент λ зависит одновременно от двух параметров - числа Re и относительной шероховатости Δ/r₀, которую можно заменить на Δ_э. Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

Третья область - область больших Re и Δ/r₀, где коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью (область расположена справа от пунктирной линии). Это область шероховатых труб, в которой все линии с различными шероховатостями параллельны между собой. Эту область называют областью автомодельности или режимом квадратичного сопротивления, т.к. здесь гидравлические потери пропорциональны квадрату скорости.

Определение λ для этой области производят по упрощенной формуле Альтшуля: