Истечение жидкости через малые отверстия в тонкой стенке при постоянном напоре

Рассмотрим большой резервуар с жидкостью под давлением Р₀, имеющий малое круглое отверстие в стенке на достаточно большой глубине Н₀ от свободной поверхности (рис.5.1).

Рис. 5.1. Истечение из резервуара

через малое отверстие Малое отверстие – отверстие, размеры которого

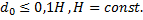
Отверстие в тонкой стенке – у стенки есть острая кромка, с которой поток срывается, а жидкость не растекается

Жидкость вытекает в воздушное пространство с давлением Р₁. Пусть отверстие имеет форму, показанную на рис.5.2, а, т.е. выполнено в виде сверления в тонкой стенке без обработки входной кромки или имеет форму, показанную на рис.5.2, б, т.е. выполнено в толстой стенке, но с заострением входной кромки с внешней стороны. Струя, отрываясь от кромки отверстия, несколько сжимается (рис.5.2, а). Такое сжатие обусловлено движением жидкости от различных направлений, в том числе и от радиального движения по стенке, к осевому движению в струе.

Рис. 5.2. Истечение через круглое отверстие

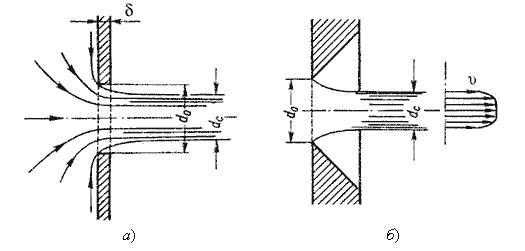
Степень сжатия оценивается коэффициентом сжатия. где Sс и Sо - площади поперечного сечения струи и отверстия соответственно; dс и dо - диаметры струи и отверстия соответственно. Скорость истечения жидкости через отверстие такое отверстие где Н - напор жидкости, определяется как φ- коэффициент скорости где α - коэффициент Кориолиса; ζ- коэффициент сопротивления отверстия. Расход жидкости определяется как произведение действительной скорости истечения на фактическую площадь сечения: Произведение ε и φ принято обозначать буквой и называть коэффициентом расхода, т.е. μ = εφ. В итоге получаем расход где ΔР - расчетная разность давлений, под действием которой происходит истечение. При помощи этого выражения решается основная задача - определяется расход. Значение коэффициента сжатия ε, сопротивления ζ, скорости φ и расхода μ для круглого отверстия можно определить по эмпирически построенным зависимостям. На рис.5.3 показаны зависимости коэффициентов ε, ζ и μ от числа Рейнольдса, подсчитанного для идеальной скорости где ν - кинематическая вязкость. При истечении струи в атмосферу из малого отверстия в тонкой стенке происходит изменение формы струи по ее длине, называемое инверсией струи (рис.5.4). Обуславливается это явление в основном действием сил поверхностного натяжения на вытекающие криволинейные струйки и различными условиями сжатия по периметру отверстия. Инверсия больше всего проявляется при истечении из некруглых отверстий.

Уравнение Бернулли (для участка 0-0 и 1-1): уравнение Бернулли примет вид: (107), a - коэффициент неравномерности; x - коэф. местного сопротивления (108). С учетом (108)(107) примет вид: (109) – фундаментальная расчетная ф-ла. Для идеал. жидкости a=1, x=0, следовательно jид.=1, тогда (110); (111) – коэффициент скорости, показывает во сколько раз скорость истечения реальной жидкости меньше скорости истечения идеальной жидкости. Коэффициент скорости для тонкой стенки j=0,97 На расстоянии l @ do/2 наблюдается сжатие: (112) – коэффициент сжатия (может быть совершенным и несовершенным, полным и неполным) Если отверстие удалено от стенок сосуда на 3- 5 d, тогда сжатие совершенно иначе несовершенного сжатия. При совершенном сжатии сжатие будет полным, у стенок – неполное сжатие. Сжатие струи – сжатие формы струи Инвестиция струи – изменение формы струи Расход в сжатом сечении: . Из (112): (113) – ур-ие связи. (114) Т.к. P=rgH, H=P/(rg) => (114) m=Q/Qид. (115) – коэффициент показывает во сколько раз расход действительной жидкости < расхода при котором скорость V=Vид. e=0,64; m=0,62; x=0,06. Все коэффициенты являются ф-ми числа рейнольца Re. Рис. 5.3. Зависимость ε, φ и от числа Reu

44. Истечение при несовершенном сжатии

Несовершенное сжатие наблюдается в том случае, когда на истечение жидкости через отверстие и на формирование струи оказывает влияние близость боковых стенок резервуара (рис.5.5).

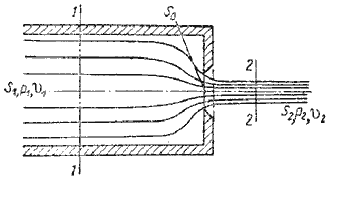
Рис. 5.5. Схема несовершенного сжатия струи

Так как боковые стенки частично направляют движение жидкости при подходе к отверстию, то струя по выходе из отверстия сжимается в меньшей степени, чем из резервуара неограниченных размеров, (как это было описано в 43 вопросе.)

При истечении жидкостей из цилиндрического резервуара круглого сечения через круглое отверстие, расположенное в центре торцевой стенки, при больших числах Re коэффициент сжатия для идеальной жидкости можно найти по формуле, представленной Н.Е. Жуковским:

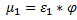
где n - отношение площади отверстия S_о к площади поперечного сечения резервуара S₁

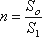
Расход жидкости при несовершенном сжатии

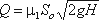
где напор Н нужно находить с учетом скоростного напора в резервуаре