
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Гидростатика изучает законы равновесия жидкости
Гидростатика изучает законы равновесия жидкости. Она рассматривает распределение давления в покоящейся жидкости, численное определение, определение направления и точки приложения силы давления жидкости на плоские и криволинейные поверхности.
Как известно, единицей давления является ньютон на квадратный метр – паскаль. Для практических вычислений эта единица неудобна, поэтому чаще применяют кратные единицы – килопаскаль (КПа) и мегапаскаль (МПа): 1 КПа = 103 Па; 1 МПа = 106 Па.
Атмосферное давление в какой-либо точке зависит от высоты этой точки над уровнем моря и незначительно колеблется в одной и той же точке. Нормальное атмосферное давление на уровне моря при температуре 0°С принимают равным рат = 101,3 КПа.
Часто жидкость сверху соприкасается с газом. Поверхность раздела между жидкостью и газообразной средой называется свободной поверхностью жидкости.
Различают абсолютное давление раб, манометрическое (избыточное) – рми вакуум – рв, между которыми существуют (рис. 1) следующие зависимости:
 , (1)
, (1)
где рат – атмосферное давление – давление между условными нулями. На рис.1 можно проследить пределы изменения разных давлений. Вакуум, например, не может быть больше атмосферного давления.
 Жидкость давит на поверхность, с которой она соприкасается. При определении силы гидростатического давления, как правило, оперируют манометрическим давлением или вакуумом, так как атмосферное давление действует на расчетную конструкцию со всех сторон, и поэтому его можно не принимать во внимание. При определении силы давления часто используется так называемая пьезометрическая плоскость или плоскость атмосферного давления – горизонтальная плоскость, проходящая через уровень жидкости в пьезометре, присоединенном к сосуду. Поверхность жидкости на уровне пьезометрической плоскости подвергается лишь воздействию атмосферного давления, т. е. рм = 0. Если сосуд с жидкостью открыт в атмосферу, то пьезометрическая плоскость совпадает со свободной поверхностью жидкости. В случае же герметично закрытого сосуда она может располагаться выше или ниже свободной поверхности. В общем случае расстояние по вертикали до пьезометрической плоскости определяется по формуле
Жидкость давит на поверхность, с которой она соприкасается. При определении силы гидростатического давления, как правило, оперируют манометрическим давлением или вакуумом, так как атмосферное давление действует на расчетную конструкцию со всех сторон, и поэтому его можно не принимать во внимание. При определении силы давления часто используется так называемая пьезометрическая плоскость или плоскость атмосферного давления – горизонтальная плоскость, проходящая через уровень жидкости в пьезометре, присоединенном к сосуду. Поверхность жидкости на уровне пьезометрической плоскости подвергается лишь воздействию атмосферного давления, т. е. рм = 0. Если сосуд с жидкостью открыт в атмосферу, то пьезометрическая плоскость совпадает со свободной поверхностью жидкости. В случае же герметично закрытого сосуда она может располагаться выше или ниже свободной поверхности. В общем случае расстояние по вертикали до пьезометрической плоскости определяется по формуле
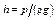 , (2)
, (2)
где r – плотность жидкости, g – ускорение силы тяжести, р – манометрическое давление или вакуум в любой точке жидкости. Расстояние h откладывается от той точки жидкости, давление в которой равно р, вверх, если оно манометрическое, и вниз – в случае вакуума.
Силу давления на плоскую поверхность можно определить аналитическим

и графоаналитическим методами. При аналитическом методе силу давления выражают формулой
 , (3)
, (3)
где рс – гидростатическое давление в центре тяжести плоской фигуры; А – площадь фигуры.
При графоаналитическом методе строят эпюры давления, выражающие закон распределения давления на контур тела, погруженного в жидкость. Сила давления равняется объему пространственной эпюры, а ее вектор проходит через центр тяжести этой эпюры. Равнодействующая сила давления жидкости на криволинейную поверхность обычно выражается тремя взаимно перпендикулярными составляющими: Fх, Fу, Fz. Горизонтальные составляющие Fхи Fувычисляют как силы давления на плоскую поверхность, равную проекции данной криволинейной поверхности на соответствующую вертикальную плоскость. Для определения вертикальной составляющей Fzстроят тела давления. При этом криволинейная поверхность проектируется вертикально на пьезометрическую плоскость. Телом давления называется тело, с одного конца ограниченное криволинейной поверхностью, с другого – пьезометрической плоскостью, а со сторон – вертикальной проектирующей поверхностью. Сила Fz равна весу жидкости, занимающей объем V тела давления:
 . (4)
. (4)
При определении сил давления жидкости на сложные поверхности часто бывает целесообразно сначала графически суммировать эпюры, а также тела давления, построенные для отдельных частей данной поверхности.
Покой жидкости относительно стенок сосуда, движущегося вместе с жидкостью, называется относительным ее покоем или равновесием. При этом отдельные частицы жидкости не смещаются одна относительно другой ився масса жидкости движется как одно твердое тело. В данном случае к силе тяжести добавляется еще другая – сила инерции, и поверхность жидкости чаще всего перестает быть горизонтальной. В относительном покое может рассматриваться, например, жидкость в перемещающейся цистерне, горючее в баке движущейся машины, жидкость во вращающемся сосуде и т.п. При вращении жидкости вместе с цилиндрическим сосудом относительно его вертикальной оси симметрии с постоянной угловой скоростью w ее поверхность под воздействием центробежных сил принимает форму параболоида вращения АВС (рис. 2), высота H которого определяется по формуле
 , (5)
, (5)
а объем параболоида
 . (6)
. (6)
Когда при вращении жидкости ее свободная поверхность пересекает дно сосуда (рис.3), показанный объем жидкости можно вычислять двояко:
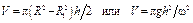 . (7)
. (7)
Дата добавления: 2015-04-18; просмотров: 220; Мы поможем в написании вашей работы!; Нарушение авторских прав |