
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов)
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся (рис.3.31).
Однако если напор, а следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.
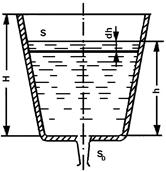
Рис. 3.31. Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

где dh - изменение уровня жидкости за время dt.
Отсюда время полного опорожнения сосуда высотой Н
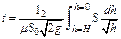
Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.3.32, стр. 134), следовательно, время его полного опорожнения
 . (3.25)
. (3.25)
Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

| 
|
| Рис. 3.32. Опорожнение призматического резервуара | Рис. 3.33. Опорожнение непризматического резервуара |
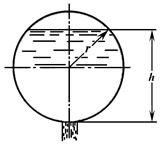
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 3.33) выразим зависимость переменной площади S от h:
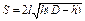
где l - длина цистерны; D - диаметр цистерны.
Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным
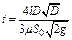 . (3.26)
. (3.26)
Дата добавления: 2015-04-18; просмотров: 251; Мы поможем в написании вашей работы!; Нарушение авторских прав |