
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Потери напора при ламинарном движении.
Как показывают исследования, при ламинарном течении жидкости в круглой трубе максимальная скорость находится на оси трубы. У стенок трубы скорость равна нулю, т.к. частицы жидкости покрывают внутреннюю поверхность трубопровода тонким неподвижным слоем. От стенок трубы к ее оси скорости нарастаю плавно. График распределения скоростей по поперечному сечению потока представляет собой параболоид вращения, а сечение параболоида осевой плоскостью - квадратичную параболу (рис. 3.10).

Рис. 3.10. Схема для рассмотрения ламинарного потока
На основе этого для потерь напора по длине при ламинарном режиме движения жидкости в трубе получено следующее уравнение:
 , (3.11)
, (3.11)
где  –абсолютный коэффициент вязкости жидкости, (кг∙с)/м2; l – длина трубопровода, м; υ – средняя скорость, м/с; γ – удельный вес жидкости, Н/м3; d – диаметр трубопровода, м.
–абсолютный коэффициент вязкости жидкости, (кг∙с)/м2; l – длина трубопровода, м; υ – средняя скорость, м/с; γ – удельный вес жидкости, Н/м3; d – диаметр трубопровода, м.
Так как 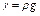 , а
, а  ,то вместо формулы (3.11) получим
,то вместо формулы (3.11) получим
 . (3.12)
. (3.12)
Выражение (3.12) называют формулой Пуазейля-Гагена (по имени ученых, получивших это уравнение).
Формула (3.12) показывает, что при ламинарном режиме потери напора пропорциональны средней скорости и не зависят от состояния стенок трубопровода.
Приравняв правые части уравнения Дарси-Вейсбаха (3.10) и выражения (3.12), получим
 . (3.13)
. (3.13)
Таким образом, коэффициент гидравлического трения при ламинарном режиме обратно пропорционален числу Рейнольдса.
Дата добавления: 2015-04-18; просмотров: 336; Мы поможем в написании вашей работы!; Нарушение авторских прав |