Уравнения Навье-Стокса

Уравнения Навье-Стокса – система дифференциальных уравнений в частных производных, описывающая движение вязкой ньютоновской жидкости. Уравнения Навье-Стокса являются одними из важнейших в гидродинамике и применяются в математическом моделировании многих природных явлений и технических задач. Названы по имени французского физика Луи Навье и британского математика Джорджа Стокса.

Система состоит из двух уравнений:

· уравнения движения,

· уравнения неразрывности.

В векторном виде для несжимаемой жидкости они записываются следующим образом:

(3.4)

где – оператор Гамильтона, Δ — оператор Лапласа, t – время, ν – коэффициент кинематической вязкости, ρ – плотность, p – давление, – векторное поле скоростей, – векторное поле массовых сил. Неизвестные p и 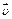являются функциями времени t и координаты , где , n = 2,3 – плоская или трехмерная область, в которой движется жидкость.

Система является математической моделью неустановившегося движения вязкой несжимаемой жидкости. В общем виде эти уравнения не могут быть решены, так как невозможно определить граничные условия в неустановившемся движении вязкой жидкости. На учете этих уравнений базируются все практические решения вопросов движения жидкости, в том числе и сквозь зернистые слои. Эти решения становятся возможными при использовании метода подобия, позволяющего из класса явлений выделить группу подобных между собой, на которые распространяются эмпирические зависимости. В этом случае математическая модель, представленная в форме дифференциальных уравнений, служит основой анализа происходящих явлений.

Обычно в систему уравнений Навье-Стокса добавляют краевые и начальные условия, например

Иногда в систему уравнений Навье – Стокса дополнительно включают уравнение теплопроводности и уравнение состояния.

При учёте сжимаемости уравнение Навье – Стокса принимает следующий вид:

где μ – коэффициент динамической вязкости, ζ – «вторая вязкость».

При решении систем уравнений Навье-Стокса необходимо учитывать ее особенности:

1. При превышении числа Рейнольдса выше некоторого критического числа, аналитическое точное решение для пространственного или плоского потока имеют хаотический вид (так называемая турбулентность). В частном случае, оно связано с теорией Фейгенбаума или другими сценариями перехода к хаосу. При уменьшении числа Рейнольдса ниже критического, решение опять принимает не хаотический вид.

2. Исключительная чувствительность к изменению коэффициентов уравнения при турбулентном режиме: при изменении числа Re на 0,05 % решения совершенно отличаются друг от друга.

3. Существует мнение, что данное уравнение является приближенным. Это обосновывается использованием при выводе уравнения Навье-Стокса линейного уравнения для нахождения давления p, как функции его нелинейных компонентов. Такая позиция обьясняет существование различных значений числа Рейнольдса (для различных частных задач), в пределах которого линейный закон осреднения корректен.

Одним из применений системы уравнений Навье – Стокса является описание течений в мантии Земли («проблема динамо»).

Вариации уравнения Навье – Стокса используются для описания движения воздушных масс атмосферы, в частности, при формировании прогноза погоды. Для описания реальных течений в различных технических устройствах приемлемую точность численного решения можно получить только при такой расчётной сетке, ячейки которой меньше самого мелкого вихря. Это требует очень больших затрат расчётного времени на современных компьютерах. Поэтому были созданы различные модели турбулентности, упрощающие расчёт реальных потоков.