Гидродинамика

Как уже было сказано, общим дифференциальным уравнением гидродинамики является система уравнений Навье-Стокса (1.2 а). Для случая, когда сила внутреннего трения приравнивается к нулю, получается дифференциальное уравнение движения идеальной жидкости (дифференциальные уравнения движения Эйлера):

;

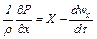; (1.7)

.

При интегрировании уравнения (1.7) получаем уравнение Бернулли для идеальной жидкости:

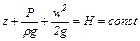, (1.8)

где z – нивелирная высота или геометрический напор. Это положение данной частицы жидкости относительно произвольно выбранной горизонтальной плоскости сравнения. Энергетический смысл: удельная потенциальная энергия положения;

– статический или пьезометрический напор. Это давление столба жидкости над рассматриваемым уровнем. Энергетический смысл: удельная потенциальная энергия давления;

– скоростной или динамический напор. Энергетический смысл: удельная кинетическая энергия в данном сечении потока;

H – полный напор или энергия жидкости, выраженная в метрах.

Энергетический смысл уравнения Бернулли звучит так. «Для любого сечения или точки потока при установившемся движении идеальной жидкости сумма потенциальной ( ) и кинетической ( ) энергий жидкостей остается величиной постоянной». Таким образом, уравнение Бернулли выражает частный случай закона сохранения энергии.

Физический смысл уравнения Бернулли: в любом поперечном сечении потока идеальной жидкости полная удельная энергия жидкости постоянна и равна H.

Реальная жидкость обладает вязкостью. Поэтому при её движении в закрытых каналах возникают касательные напряжения вследствие трения слоев жидкости между собой и о стенки канала. Кроме того, движение вязкой жидкости часто сопровождается вращением частиц, вихреобразованием и перемешиванием, особенно в местах, где происходит изменение живого сечения или направления движения потока.

Все это требует затраты энергии, поэтому удельная энергия при движении вязкой жидкости не остается постоянной. С учетом неравномерного распределения скоростей по сечению потока и потерь энергии на преодоление сопротивления уравнение Бернулли для реальной (вязкой) жидкости приобретает вид:

, (1.9)

где – величина гидравлического сопротивления или энергия, затрачиваемая на преодоление гидравлического сопротивления. Ее еще называют «потерянный напор».

Данное уравнение используется для описания движения реальной жидкости и расчета гидравлических потерь, как от трения, так и от местных сопротивлений.

Потери напора (энергии) на преодоление гидравлических сопротивлений или, как их часто называют, гидравлические потери зависят от формы, размеров русла, скорости течения и вязкости жидкости. При этом вязкость жидкости, хотя и является первопричиной всех гидравлических потерь, но далеко не всегда оказывает существенное влияние на их величину.

Как показывают опыты, гидравлические потери, как правило, пропорциональны скорости течения жидкости во второй степени:

, (1.10)

где ξ – безразмерный коэффициент пропорциональности, называемый коэффициентом потерь или коэффициентом сопротивления.

Физический смысл коэффициента потерь заключается в отношении потерянного напора к скоростному.

Гидравлические потери обычно разделяют на местные потери и потери на трение по длине:

∑h_n = h_{м +} h_тр. (1.11)

Местные потери h_м обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы, размеров или направлениями русла, вызывающими деформацию потока.

Потери на трение обусловлены вязкостным трением слоев жидкости между собой и о стенки канала. Они возникают в прямых трубах постоянного сечения, т.е. при равномерном течении, и возрастают пропорционально длине трубы.

Таким образом, гидравлическое сопротивление однофазных потоков можно найти из уравнений:

(1.12)

или . (1.13)

Величину гидравлических сопротивлений необходимо знать для определения движущей силы гидромеханических (гидравлических) процессов – разности давлений между двумя точками или сечениями аппарата. Кроме этого, величина h_n необходима для определения оптимального диаметра трубопровода .