
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные определения. Метод анализа размерностей часто бывает очень эффективен при решении сложных задач механики, в частности
Метод анализа размерностей часто бывает очень эффективен при решении сложных задач механики, в частности, в гидродинамике и аэродинамике. Совместно с представлениями о физическом смысле явлений или с привлечением опытных данных он приводит, и притом быстро и просто, к результатам, дающим предварительную ориентировку в рассматриваемом круге явлений.
Существует несколько систем единиц измерений и в каждой из них некоторые физические величины условно принимаются за основныеилипервичные, т.е. такие, для которых единицы устанавливаются произвольно и независимо. В механике, и в частности, в гидромеханике и гидравлике применяется система L, m, t,в которой за основные величины принимаются длина L, масса m и время t. Очевидно, что при анализе любого явления единицы измерения массы, времени и длины выбираются независимо друг от друга. Ко вторичным величинам относятся те, которые получаются как комбинации основных. Например, ко вторичным величинам относятся: скорость V=S/t или [V]=Lt -1, ускорение a=V/t или [a]=Lt-2, плотность ρ=m/W или [ρ]=mL-3 и многие другие величины. Квадратные скобки, в которые поставлено обозначение величины, означает, что речь идет о размерности единицы этой величины, а символы L,m,t представляют собой обобщенные обозначения единиц длины, массы и времени без указания конкретного наименования единиц. Понятие размерности возникает в связи с требованием, чтобы в одной и той же системе основных единиц количественные соотношения между различными физическими величинами – например, между напором H и скоростью истечения V, длиной маятника l и периодом T его колебаний - выражались одними и теми же формулами независимо от выбора масштаба единиц основных физических величин (т.е. например, на вид зависимости для скорости истечения не влияет, в сантиметрах или в метрах измеряется напор H).
В специальных курсах показывается, что формула размерности вторичных величин должна быть степенного вида относительно всех основных физических величин. Допустим, например, что число основных величин выбрано равным трем и за них приняты длина L, масса m и время t. Тогда размерность физической величины y представится формулой
[y]=Lpmq t r , (1.1)
где p, q, r – постоянные числа (напомним, что квадратные скобки, в которые поставлен символ величины y, означает, что рассматривается размерность этой величины). Формула (1.1) называется формулой размерности единицы данной величиныили, как часто говорят, кратко- размерностью данной величины.
Необходимо подчеркнуть, что умножать и делить можно физические величины любой размерности, а складывать и вычитать возможно только величины одинаковой размерности.
Пример 1.1.Скорость V может быть выражена как V=L/t=L1 m 0 t -1, т.е. p=1, q=0, r= -1.Сила F=ma может быть представлена как F=mL/t²=
= L1 m1 t -2, т.е. p=1, q=1,r= -2.
Не обязательно p, q, r – рациональные числа, но вводить числа кроме рациональных нет необходимости. Часто размерность физической величины отождествляют с ее единицей в соответствующей системе единиц. Так, например, говорят, что скорость имеет размерность см/с (сантиметр в секунду). Хотя это и не логично, но грубой ошибки в этом нет. В данном случае см/с- это наименованиеединицы (точно так же, как км/ч, м/с и т.д.).Всегда, если есть необходимость, единицы такого типа позволяют перейти к формулам размерности, в которых масштабы единиц основных величин не фиксированы.
Замечание 1.1.Разные физические величины могут иметь одинаковые размерности даже в одной и той же системе единиц. Примерами могут служить в механике работа и кинетическая энергия или работа и момент силы (система Lmt).
Замечание 1.2. Безразмерными комбинациями физических величин называются такие комбинации, которые в рассматриваемой системе единиц имеют нулевую размерность.Их числовые значения не меняются при изменении масштабов единиц основных величин.
Задача 1.1.Найти размерности: 1) давления; 2) энергии; 3) коэффициента динамической вязкости; 4) коэффициента кинематической вязкости; 5) коэффициента поверхностного натяжения; 6) отношения Р\ρg .
Решение.Размерности величин всегда определяются по соответствующим формулам, например, размерность давления определяется из отношения, которое служит определением давления
p = 
 ,
,
где F – сила; S – площадь. Размерность силы [F] = mLt-2, площади [S] = L2. Тогда
[p] =  =
=  = mL-1t-2.
= mL-1t-2.
Размерность энергии E совпадает с размерностью работы, т.е.
[Е] = [А].
Работа А может быть определена по формуле
А = F·l,
где F – сила; l – расстояние. Тогда
 .
.
Коэффициент динамической вязкости входит в формулировку закона вязкости Ньютона
F = μS  ,
,
где F – сила; μ – коэффициент динамической вязкости; S – площадь; dU/dl – градиент скорости. Коэффициент μ выразится из последней зависимости так
μ =  .
.
Размерности величин, входящих в зависимость для μ,такие

 , [S] = L2, [dU/dl] = t-1.
, [S] = L2, [dU/dl] = t-1.
Окончательно

Для определения размерности кинематического коэффициента вязкости ν используем зависимость
μ = ρν,
где ρ – плотность жидкости. Размерность плотности находится из формулы
ρ =  ,
,
где W –объем. Имеем далее

и тогда
 .
.
Размерность коэффициента поверхностного натяжения определяется из формулы
 ,
,
где F – сила; l – длина. Тогда
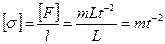 .
.
Дата добавления: 2015-04-18; просмотров: 227; Мы поможем в написании вашей работы!; Нарушение авторских прав |