
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Размерности обеих частей равенства должны быть одинаковы.
В таком виде эта теорема получила название правила размерностей. В равенство типа A=B могут входить также в качестве множителей либо постоянные коэффициенты, либо безразмерные комбинации физических величин.
Пример 2.1.Необходимо найти вид зависимости для объема шара.
Шар полностью определяется заданием его радиуса, поэтому объем его W равен W=f(R), где f(R)- функция, подлежащая определению. Так как R измеряется, например, в метрах (м), а W в кубических метрах (м3), то задача сводится к нахождению математической операции «превращающей» метры линейные в метры кубические. Ясно, что существует одна операция такого рода- возведение в третью степень. Заключаем, что искомая зависимость имеет вид W=CR³, где C- некоторое число, не зависящее от R (постоянный безразмерный коэффициент). В этом примере впервые вводится постоянный безразмерный коэффициент С; везде в дальнейшем необходимо помнить, что он может быть функцией некоторых параметров и даже первичных величин. Единственное, что можно утверждать заранее – что С является всегда безразмерной величиной и в виде сомножителя не нарушает размерности правой части. Если C не зависит от R, то достаточно лишь для одного шара любого радиуса найти отношение W/R³ (каким-либо измерением), которое будет равно ≈ 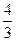 π ≈ 4,189. В дальнейшем можно будет определить объем шара с помощью зависимости W=4,19R³.
π ≈ 4,189. В дальнейшем можно будет определить объем шара с помощью зависимости W=4,19R³.
Теория размерностей без привлечения дополнительных данных не может привести ни к каким физическим зависимостям, поскольку в ее основы не заложено никаких физических законов. Для того, чтобы получить с помощью этой теории конкретные выводы, необходимо установить,между какими физическими величинами существуют количественные связи.На этот вопрос теория размерности не может дать никакого ответа. Это можно сделать только либо опытным путем, либо с помощью каких-то физических законов. Приведенные ниже примеры и задачи служат иллюстрацией сказанного. Вначале для лучшего понимания метода анализа размерностей приводятся простые примеры из механики.
Пример 2.2.Тело начинает движение из состояния покоя и движется с постоянным ускорением a. Найти вид зависимости для пути, проходимого телом.
Путь, проходимый телом, прежде всего, конечно, является функцией времени. Кроме того, он будет зависеть от ускорения, которое задано. Если включить в число параметров массу тела m, то необходимо учесть соотношение F = ma и таким образом включить в рассмотрение также и силу, действующую на данное тело. Возможно допустить воздействие на тело любых сил (сил сопротивления разной природы, движущих сил – внешних и внутренних и т.д.), но при заданной массе m их отношение  и будет выражать ускорение.
и будет выражать ускорение.
Таким образом, при заданном ускорении формулировка задачи не выводит ее из класса кинематических задач; окончательный вид функциональной зависимости для пути
S = f (a,t)
и функция f (a,t) должна иметь размерность длины, т.е.
[S (a,t)] = [S] = L.
Согласно первой теореме функция f(a,t) является степенной относительно своих аргументов, т.е. имеет вид
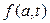 =
=  ,
,
где C, 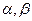 - некоторые постоянные. Таким образом, искомая функция имеет вид
- некоторые постоянные. Таким образом, искомая функция имеет вид
S=Ca  ,
,
причем  и
и 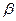 такие, что выполняется условие
такие, что выполняется условие
L=[a 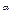 t
t 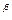 ]. (2.1)
]. (2.1)
Обычно следующим шагом является выражение всех входящих в правую часть (2.1) величин через основные; в данном случае это необходимо сделать для ускорения a:[a]=L/t 2=Lt –2. Тогда из (2.1) следует
L=(Lt –2) 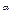 t
t 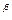 .
.
Раскроем в последнем равенстве скобки
L=L 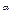 t
t  t
t 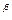
и заметим, что в правой части последнего равенства присутствует время t, а в левой части его нет. Поэтому в левой части представляем сомножитель t0 (он равен единице) который ничего не меняет:
L1t0=L 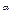 t
t 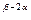 .
.
Совершенно ясно, что если какая-либо величина находится одновременно в правой и левой части равенства типа (2.1), то показатель степени ее в левой части равен показателю степени в правой части. Например, при применении этого правила к последнему равенству будем иметь:
для показателей степеней у L
1= 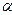
для показателей степеней у t
0=  .
.
Величины  и
и 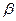 находим из системы уравнений
находим из системы уравнений
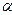 =1
=1
 =0.
=0.
Показатели степеней равны 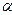 =1,
=1, 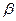 =2.
=2.
Дата добавления: 2015-04-18; просмотров: 269; Мы поможем в написании вашей работы!; Нарушение авторских прав |