Параллельное соединение

При параллельном соединении участков трубопровода жидкость, подходя с расходом Q к точке их разветвления А, распределяется по ответвлениям и далее снова собирается в точке их соединения В (рис. 11.6). При параллельном соединении обычно заданы: 1) Суммарный расход до точки разветвления; 2) Длина, диаметр, величина к_э каждой ветви и все коэффициенты ζ_i . Основными задачами гидравлического расчета в этом случае являются: 1. Определение расходов Q₁, Q₂, Q₃, …, Q_n на отдельных участках, соединенных параллельно. 2.Определение потерь напора Δh между точками А и В на каждом участке.

При решении задачи, прежде всего, учтем очевидное условие: равенство расхода Q сумме всех расходов

Q = Q₁ + Q₂ + Q₃ + … + Q_n . (11.15)

Для дальнейшего решения представим, что в точках А и В установлены пьезометры; так как концы всех трубопроводов смыкаются в одних и тех же точках А и В, то потери на всех этих участках одинаковы и равны Δh (Δh - разность показаний пьезометров, установленных в точках А и В).Поэтому справедливы следующие равенства

Δh=Δh₁=Δh₂=Δh₃= …= Δh_n . (11.16)

Решая систему уравнений (11.16), можно выразить все расходы через один (например, через Q₁)и, подставив затем эти значения расходов в (11.15), найти Q₁. После этого с помощью (11.16) определяют последовательно расходы Q₂, Q₃, ..., Q_n , а по любому из уравнений системы (11.16) определяют потери напора Δh.

Задача 11.6. Определить расходы и потери напора в каждой из n параллельно соединенных ветвей, считая, что как местные сопротивления, так и сопротивления по длине - в квадратичной области.

Решение. В общем случае имеем для потерь в каждой ветви

(11.17)

Имеем также Q=Q₁+Q₂+Q₃+…+ Q_n. (11.18)

Примем обозначения .

тогда уравнения (11.17) перейдут в такие

.(11.19)

Из последнего уравнения выражаем все расходы через один, например Q₁

.(11.20)

Затем из (11.18) получаем

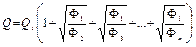. (11.21)

Решая последнее уравнение относительно Q₁, определим его значение, а из (11.21) и все остальные расходы; по любой из зависимостей (4.6) находим h_w.