
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критическая глубина
Выражение для удельной энергии сечения в открытых руслах можно представить в следующем виде (учитывая, что V=Q/S)
Э  , (14.1)
, (14.1)

 где h – глубина; Q – расход; S – площадь сечения при данной глубине;
где h – глубина; Q – расход; S – площадь сечения при данной глубине;  - коэффициент, учитывающий неравномерность распределения скоростей.
- коэффициент, учитывающий неравномерность распределения скоростей.
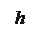
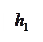

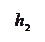
 Из (14.1) видно, что при заданном расходе в данном русле удельная энергия сечения является функцией глубины, т.е. Э=f(h).
Из (14.1) видно, что при заданном расходе в данном русле удельная энергия сечения является функцией глубины, т.е. Э=f(h).
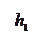
 При этом: 1) если h
При этом: 1) если h  0, то
0, то
|
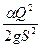

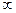 и, следовательно, Э
и, следовательно, Э 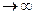 , 2)если
, 2)если  , то
, то 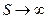 и
и  .
.
 График функции
График функции  имеет вид, как на рис. 14.1; из графика видно, что функция
имеет вид, как на рис. 14.1; из графика видно, что функция  выражается кривой, состоящей из двух ветвей, разделяемых точкой А, соответствующей минимуму
выражается кривой, состоящей из двух ветвей, разделяемых точкой А, соответствующей минимуму  . При этом нижняя ветвь асимптотически приближается к оси абсцисс, а верхняя ветвь - к прямой, проходящей через начало координат и составляющей с осью
. При этом нижняя ветвь асимптотически приближается к оси абсцисс, а верхняя ветвь - к прямой, проходящей через начало координат и составляющей с осью
абсцисс угол 45о. Так как кривая непрерывна, то при некотором значении глубины h, где-то удельная энергия будет иметь наименьшее значение 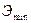 .
.
Глубина потока, при которой удельная энергия сечения принимает минимальное значение, называется критической глубиной 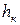 .
.
Для нахождения величины  необходимо решить уравнение
необходимо решить уравнение
 .
.
Так как 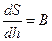 - ширина живого сечения, то уравнение для определения критической глубины будет таким
- ширина живого сечения, то уравнение для определения критической глубины будет таким
 , (14.2)
, (14.2)
где  и
и 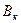 - площадь сечения и ширина русла по верху, отвечающие критической глубине hк.
- площадь сечения и ширина русла по верху, отвечающие критической глубине hк.
Уравнение (14.2) является основной зависимостью для определения критической глубины 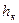 при заданном расходе Q и любой заданной форме русла; из этого уравнения следует, что при заданном расходе критическая глубина зависит только от размеров и формы живого сечения. Критическая глубина не зависит ни от уклона дна, ни от шероховатости.
при заданном расходе Q и любой заданной форме русла; из этого уравнения следует, что при заданном расходе критическая глубина зависит только от размеров и формы живого сечения. Критическая глубина не зависит ни от уклона дна, ни от шероховатости.
Прямоугольное русло. Для прямоугольного русла шириной  =В критическую глубину возможно найти аналитически. При критической глубине
=В критическую глубину возможно найти аналитически. При критической глубине 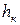 площадь сечения
площадь сечения
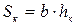 .
.
Подставляя  в (14.2), получим
в (14.2), получим
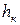 =
=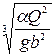 .(14.3)
.(14.3)
Задача 14.1. Определить критическую глубину для трапецеидального канала при следующих данных:  =5 м, т=1,5 м; расход воды в канале Q=6,6 м3/ч.
=5 м, т=1,5 м; расход воды в канале Q=6,6 м3/ч.
Решение.Вычисляем значение правой части (14.2) при  ,
,
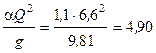 м5.
м5.
Задаваясь затем различными глубинами h, находим ширину по верху  , площадь сечения
, площадь сечения 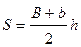 и S3. Результаты этих подсчетов сводим в табл. 14.1.
и S3. Результаты этих подсчетов сводим в табл. 14.1.
Таблица 14.1
| h, м | B, м | S, м2 | S3 м6 |  м5 м5
|
| 0,50 | 6,5 | 2,81 | 3,68 | 3,68<4,9 |
| 0,60 | 6,8 | 3,54 | 6,52 | 6,52>4,9 |
| 0,55 | 6,65 | 3,20 | 4,94 | 4,94  4,9 4,9
|
Дата добавления: 2015-04-18; просмотров: 288; Мы поможем в написании вашей работы!; Нарушение авторских прав |