
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Критический уклон. Спокойные и бурные потоки
Ранее отмечалось, что критическая глубина не зависит от уклона дна. Между тем нормальная глубина (при равномерном движении) зависит от уклона. Очевидно, что при некотором уклоне можно получить нормальную глубину, численно равную критической.
Уклон дна, при котором нормальная глубина равна критической глубине, называется критическим уклоном.
Очевидно, что при критическом уклоне и критической глубине может иметь место равномерное движение, причем формула для определения расхода в этом случае будет иметь вид
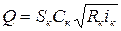 .
.
Представляя зависимость для Q в (14.2), получим
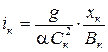 , (15.1)
, (15.1)
где  – смоченный периметр при глубине, равной критической.
– смоченный периметр при глубине, равной критической.
Необходимо помнить, что при изменении расхода Q изменяется и критический уклон iк; следовательно, данный уклон дна, который является критическим для данного расхода, перестает быть критическим при ином расходе.
Отметим, что при уклоне дна русла i меньше критического iк (i<iк) нормальная глубина больше критической (h0>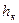 ). При уклоне дна i больше критическогоiк (i>iк) нормальная глубина h0 меньше критической (h0<
). При уклоне дна i больше критическогоiк (i>iк) нормальная глубина h0 меньше критической (h0<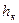 ).
).
Критическая глубина, а следовательно и критический уклон могут служить критерием для характеристики состояния потока.
Так, движение воды при глубинах потока больше критической (h>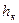 ) (i<iк) принято называть спокойным состоянием (спокойные потоки), а при глубинах потока меньше критической (h<
) (i<iк) принято называть спокойным состоянием (спокойные потоки), а при глубинах потока меньше критической (h<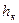 ) (i>iк) – бурным состоянием (бурные потоки).
) (i>iк) – бурным состоянием (бурные потоки).
При глубине потока, равной критической глубине h=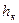 , поток находится в критическом состоянии.
, поток находится в критическом состоянии.
На рис. 14.1 показаны области значений величин h и Э, при которых движение будет бурным или спокойным, причем нижняя ветвь кривой удельной энергии сечения Э=f(h) может быть названа ветвью бурного состояния, а верхняя ветвь – ветвью спокойного состояния потока.
Задача 15.1. Определить критический уклон для земляного канала, имеющего трапецеидальную форму сечения при следующих данных:  =5,0 м, т=1,5 м; расход воды в канале Q=6,6 м3/ч, hк=0,55 м, Вк=6,65 м, Sк=3,2 м2 и n=0,030.
=5,0 м, т=1,5 м; расход воды в канале Q=6,6 м3/ч, hк=0,55 м, Вк=6,65 м, Sк=3,2 м2 и n=0,030.
Решение.Смоченный периметр при hк=0,55 м определяется по формуле  м. Гидравлический радиус
м. Гидравлический радиус 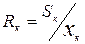 =3,2/6,98=0,46 м. При n=0,03 и Rк=0,46 м по формуле Павловского находим Ск=27,1. По формуле (15.1) находим критический уклон iк=0,0126.
=3,2/6,98=0,46 м. При n=0,03 и Rк=0,46 м по формуле Павловского находим Ск=27,1. По формуле (15.1) находим критический уклон iк=0,0126.
Дата добавления: 2015-04-18; просмотров: 279; Мы поможем в написании вашей работы!; Нарушение авторских прав |