Основные расчетные зависимости и методика расчета. 1) Истечение жидкости при постоянном напоре

1) Истечение жидкости при постоянном напоре

Расчет заключается в определении расхода, действующего напора или размеров отверстия (насадка).

Основная расчетная формула: 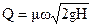, (6.1)

где μ – коэффициент расхода;

ω – площадь поперечного сечения отверстия (насадка);

Н – действующий напор.

Значения коэффициента μ для малого круглого отверстия в тонкой стенке при совершенном сжатии можно найти из графика /1/, предварительно вычислив число Рейнольдса по теоретической скорости V_т = √2gH. При значениях Re_т > 10⁵ в расчетах принимают μ = 0,62.

При несовершенном сжатии коэффициент расхода отверстия определяется согласно рекомендациям /1, 2, 3, 5, 6/.

Коэффициент расхода цилиндрического насадка зависит от отношения l/d и числа Re и может быть найден по эмпирической формуле:

μ = 1/[1,23 + (68/Re)l/d]. (6.2)

Для оптимальной длины насадка принимают μ = 0,82.

При решении задачи с учетом d, Н, п (здесь п – расстояние от стенки до отверстия) устанавливают тип отверстия, вид сжатия и определяют μ.

2) Истечение при переменном напоре

Определяется время изменения уровня жидкости в резервуаре (бассейне) от Н₁ до Н₂ или его полного опорожнения.

Для случая истечения в атмосферу расчетная формула для определения времени t имеет вид /1, 2/:

t = 2Ω(√H₁ - √H₂)/μω√2g, (6.3)

где Ω – площадь поперечного сечения призматического резервуара;

Н₁, Н₂ – соответственно начальный и конечный напоры;

μ – коэффициент расхода отверстия (насадка);

ω – площадь поперечного сечения отверстия (насадка).

Для случая истечения через отверстие (насадок) при переменном (уменьшающемуся во времени) напоре под переменный уровень следует пользоваться расчетными формулами, рекомендованными в литературе.