
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Помехоустойчивое кодирование
 Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющее его прием. Ниже приведена классификация помех и их источников.
Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющее его прием. Ниже приведена классификация помех и их источников.
Внешние источники помех вызывают в основном импульсные помехи, а внутренние - флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевые и дробления. Краевыеискажения связаны со смещением переднего или заднего фронта импульса. Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов.
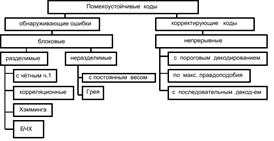 Приведем классификацию помехоустойчивых кодов.
Приведем классификацию помехоустойчивых кодов.
Построение помехоустойчивых кодов в основном связано с добавлением к исходной комбинации (k-символов) контрольных (r-символов) см.на рис.5.1. Закодированная комбинация будет составлять n-символов. Эти коды часто называют (n,k) - коды.
k—число символов в исходной комбинации
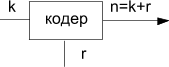 r—число контрольных символов
r—число контрольных символов
Рис.5.1. Получение(n,k)-кодов.
Надёжность электронных устройств по мере их совершенствования всё время возрастает, но, тем не менее, в их работе возможны ошибки, как систематические, так и случайные. Сигнал в канале связи может быть искажён помехой, поверхность магнитного носителя может быть повреждена, в разъёме может быть потерян контакт. Ошибки аппаратуры ведут к искажению или потере передаваемых или хранимых данных. При определённых условиях, некоторые из которых рассматриваются в этом разделе, можно применять методы кодирования, позволяющие правильно декодировать исходное сообщение, несмотря па ошибки в данных кода. В качестве исследуемой модели достаточно рассмотреть канал связи с помехами, потому что к этому случаю легко сводятся остальные. Напри- мер, запись на диск можно рассматривать как передачу данных в канал, а чтение с диска — как приём данных из капала.
Вторая теорема Шеннона.
Вторая теорема Шеннона Если производительность источника R ≤ C – ε, где ε – сколь угодно малая положительная величина, то существует способ кодирования, позволяющий передать все сообщения источника со сколь угодно малой вероятностью ошибки.
Если производительность информационной системы меньше пропускной способности канала, то сообщение от этого источника можно преобразовать так, чтобы передавать их по каналу с помехами с любой степенью точности, т. е. за счет существования избыточности в сообщениях, вводимой специальным образом, можно уменьшить вероятность ошибки до сколь угодно малой величины.
С точки зрения технической реализации эта теорема означает, что существует способ кодирования и декодирования, при котором вероятность ошибочного декодирования может быть сколь угодно малой. Если R > С, то таких способов не существует.
Код Хемминга.
Код Хэмминга, являющийся групповым (n,k) кодом, с минимальным расстоянием d=3 позволяет обнаруживать и исправлять однократные ошибки. Для построения кода Хэмминга используется матрица H. 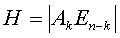 , где Ak- транспонированная подматрица, En-k - единичная подматрица порядка n-k.
, где Ak- транспонированная подматрица, En-k - единичная подматрица порядка n-k.
Если Х - исходная последовательность, то произведение Х·Н=0. Пусть E- вектор ошибок. Тогда (Х+Е)·Н = Х·Н+Е·Н = 0+Е·Н=E·H - синдром или корректор, который позволяет обнаружить и исправить ошибки. Контрольные символы e1 ,e2 ,...,er образуются из информационных символов, путем линейной комбинации 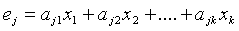 , где аj={0,1} - коэффициенты, взятые из подматрицы A матрицы H.
, где аj={0,1} - коэффициенты, взятые из подматрицы A матрицы H.
Дата добавления: 2015-04-18; просмотров: 298; Мы поможем в написании вашей работы!; Нарушение авторских прав |