Модели шифров.

Алгебраическая модель шифров:

– конечные множества возможных открытых текстов, ключей и шифрованных текстов;

–правило зашифрования на ключе , - множество правил зашифрования.

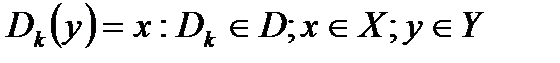–правило зашифрования на ключе , - множество правил расшифрования.

Если представляется в виде k =(k₃, k_р) где k₃— ключ зашифрования, а k₃— ключ расшифрования (причем k₃ k_р), то Е_kпонимается как функция Е_k3,а D_k — как функция D_kp.

Модель шифра: сово­купность со свойствами:

1. (однозначность расшифрования) В то же время x может соответствовать нескольким y.

2.

Из условия 1 следует инъективность функции :

Шифр перестановки: Пусть и пусть , где - симметрическая группа подстановок множества (Грубо говоря, L – количество символов из алфавита A в шифруемом блоке). Для любого ключа k, открытого текста и шифрованного текста правила шифрования и расшифрования определяются формулами:

Шифр простой замены: Пусть , , где — симметрическая группа подстановок множества А. X и Y представляют собой объединения декартовых степеней множества А. Для любого ключа , открытого текста и шифрованного текста правила шифрования и расшифрования шифра простой замены в алфавите А определяются формулами:

В общем случае могут быть разными.

Вероятностная модель шифров:

Определим априорные распределения вероятностей P(X), P(K) на множествах Х и K соответственно. Тем самым для любого определена вероятность и для любого — вероятность , причем выполняются равенства: Тогда вероятностная модель выглядит следующим образом:

Блочные шифры осуществляют преобразования блоками данных фиксированной длины.

Поточные шифры осуществляют преобразование каждого бита информации в зависимости от его позиции в шифруемом тексте и ключа шифрования.

Различают симметричные (ключи шифрования и расшифрования одинаковы) и асимметричные (ключи разные, один из которых является секретным, другой открытым) криптосистемы.

Ключевая система определяет порядок использования криптографической системы и включает системы установки и управления ключами.

Система установки ключей – определяет алгоритмы и процедуры генерации, распределения, передачи и проверки ключей.

Система управления ключами – определяет порядок использования, смены, хранения и уничтожения ключей.

Основные требования к шифрам:

В секрете держится только определенный набор параметров алгоритма (ключ), а остальные детали могут быть открыты без снижения стойкости алгоритма ниже допустимой величины.

Длина блока при блочном шифровании должна быть достаточной для того, чтобы исключить возможность статистического анализа.

Длина ключа должна быть достаточной, чтобы исключить возможность анализа с помощью перебора всех вариантов ключей.

Зависимость шифрованного текста от открытого текста и от ключа должна быть сложной и неочевидной (конфузия).

Изменение каждого бита ОТ и каждого бита ключа должны менять каждый бит ШТ с вероятностью близкой к ½ (диффузия).

Алгоритмы шифрования и расшифрования должны быть известными.

Функции шифрования и расшифрования должны быть легко вычислимы для любых текстов, если известен ключ/ключи, и трудно вычислимы в ином случае.

Вычисление ключей шифрования/расшифрования при наличии некоторого набора пар ОТ-ШТ, а также вычисление ключа шифрования из ключа расшифрования и наоборот (при атаке на шифр, а не при создании ключей) должно быть трудной вычислительной задачей.

59. Системы шифрования с открытыми ключами: RSA, системы Эль-Гамаля, системы на основе «проблемы рюкзака».

Концепция криптографии с открытым ключом заключается в том, что для зашифрования и расшифрования используются разные ключи, причем зная значение одного ключа нельзя получить значение другого.

RSA.

Общая схема алгоритма:

1) каждый пользователь генерирует пару ключей: один для зашифрования и один для расшифрования;

2) пользователи публикуют ключи зашифрования в открытом доступе, а второй ключ, соответствующий открытому, сохраняется в секрете;

3) посылая пользователю В сообщение, пользователь А зашифровывает его открытым ключам пользователя В;

4) пользователь В расшифровывает полученное сообщение с помощью своего секретного ключа.

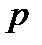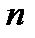Пользователь выбирает простые числа и , вычисляет и выбирает число , взаимно простое с , где - функция Эйлера (равна количеству целых чисел, меньших и взаимно простых с ). Далее находим число , обратное относительно умножения к : . Ключ является ключом шифрования, ключ является ключом расшифрования. Шифрующее преобразование: , расшифровывающее преобразование: . Легко заметить, что

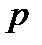В зависимости от поставленной задачи (шифрование / ЭЦП), один из ключей , засекречивается, а второй помещается в общий доступ. Криптостойкость данной системы основана на сложности разложения числа на простые множители и . Для обеспечения лучшей криптостойкости числа 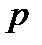и должны различаться по размеру на несколько десятичных разрядов, иметь небольшой НОД (в идеале 1) и каждое из них должно иметь хотя бы один большой простой делитель.

ElGamal.

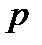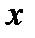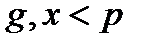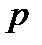Безопасность алгоритма основана на трудности вычисления дискретных логарифмов в конечном поле. Для генерации пары ключей сначала выбирается простое число и два случайных числа, и : . Затем вычисляется . Открытым ключом являются , и . И и 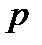можно сделать общими для группы пользователей. Закрытым ключом является 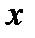. Для шифрования сообщения М сначала выбирает­ся случайное число , взаимно простое с . Затем вычисляются и . Пара является закрытым шифртекстом. Для расшифрования вычисляют: .

Система на основе «проблемы рюкзака».

Безопасность алгоритмов рукзака опирается на NP-полную проблему. Проблем рюкзака заключается в следующем: пусть дан набор значений M­₁,M₂,…,M_n и сумма S. Необходимо найти значения b_iтакие, что: , где может быть либо нулем, либо единицей. Существует 2 проблемы рюкзака. Проблема рюкзака является «Легкой», если перечень значений (M_i) представляет собой сверхвозрастающую последовательность (когда каждый член больше суммы всех предыдущих). Решение заключается в сравнении суммы (S) с самым большим числом последовательности. Если S больше, либо равен этому числу (M_i), то b_iпринимают за «1». Уменьшаем S на значение M_i и переходим к следующему числу последовательности. Процесс повторяется, пока последовательность не закончится. Если по окончании S равно нулю, то решение найдено. Проблема рюкзака является «Трудной», если перечень значений (M_i) – не сверхвозрастающая последовательность. Алгоритма быстрого решения не найдено.

В основу алгоритма рюкзака Меркла-Хеллмана лежит идея шифровать сообщение, как решение набора проблем рюкзака. Сверхвозрастающая последовательность рюкзака является закрытым ключам, а нормальная – открытым.

Для шифрования данных используется нормальная последовательность, которая получается из сверхвозрастающей следующим образом: Здесь - член сверхвозрастающей последовательности, - полученный член нормальной последовательности для шифрования, - число, большее суммы элементов сверхвозрастающей последовательности, k- число, взаимно простое с .

Для шифрования данные разбиваются на блоки по n бит. Считается сумма , которая является шифрованным текстом. Нормальная последовательность является открытым ключом шифрования.

Для расшифрования необходимо знать числа и . Шифрованный текст преобразуется: , где преобразуется алгоритмом расшифровки сверхвозрастающего рюкзака в исходную последовательность бит.

Реальные рюкзаки должны содержать не менее 250 элементов. Длина каждого члена сверхвозрастающей последовательности должна быть где-то между 200 и 400 битами, а длина модуля должна быть от 100 до 200 битов. В таком случае, полный перебор для взлома будет бессмысленным. На сегодняшний день существуют алгоритмы достаточно быстрого взлома оригинальной схемы и большинства её модификаций. Также есть варианты алгоритма рюкзака, считающиеся безопасными на сегодняшний день.

Цифровая подпись. Общие положения. Цифровые подписи на основе шифросистемы с открытыми ключами стандартов ГОСТ Р и DSS.

Цифровая подпись (сообщения или электронного документа) --- представляет собой конечную цифровую последовательность, зависящую от самого сообщения или документа и от секретного ключа, известного только подписывающему субъекту, предназначенная для установления авторства. Предполагается, что цифровая подпись должна быть легко проверяемой без получения доступа к секретному ключу. При возникновении спорной ситуации, связанной с отказом подписывающего от факта подписи некоторого сообщения либо с попыткой подделки подписи, третья сторона должна иметь возможность разрешить спор. Цифровая подпись позволяет решить следующие три задачи: осуществить аутентификацию источника данных, установить целостность сообщения или электронного документа, обеспечить невозможность отказа от факта подписи конкретного сообщения.

1) электронная цифровая подпись — набор электронных цифровых символов, созданный средствами электронной цифровой подписи и подтверждающий достоверность электронного документа, его принадлежность и неизменность содержания;

2) электронный документ — документ, в котором информация представлена в электронно-цифровой форме и удостоверена посредством электронной цифровой подписи;

3) владелец регистрационного свидетельства — физическое или юридическое лицо, на имя которого выдано регистрационное свидетельство, правомерно владеющее закрытым ключом, соответствующим открытому ключу, указанному в регистрационном свидетельстве;

4) закрытый ключ электронной цифровой подписи — последовательность электронных цифровых символов, известная владельцу регистрационного свидетельства и предназначенная для создания электронной цифровой подписи с использованием средств электронной цифровой подписи;

5) открытый ключ электронной цифровой подписи — последовательность электронных цифровых символов, доступная любому лицу и предназначенная для подтверждения подлинности электронной цифровой подписи в электронном документе;

6) подписывающее лицо — физическое или юридическое лицо, правомерно владеющее закрытым ключом электронной цифровой подписи и обладающее правом на ее использование на электронном документе;

7) регистрационное свидетельство — документ на бумажном носителе или электронный документ, выдаваемый удостоверяющим центром для подтверждения соответствия электронной цифровой подписи требованиям, установленным настоящим Законом;

8) система электронного документооборота — система обмена электронными документами, отношения между участниками которой регулируется настоящим Законом и иными нормативными правовыми актами Республики Казахстан;

9) средства электронной цифровой подписи — совокупность программных и технических средств, используемых для создания и проверки подлинности электронной цифровой подписи;

10) удостоверяющий центр — юридическое лицо, удостоверяющее соответствие открытого ключа электронной цифровой подписи закрытому ключу электронной цифровой подписи, а также подтверждающее достоверность регистрационного свидетельства;

Общие положения

1. Цифровая (электронная) подпись предназначена для обеспечения подтверждения подлинности и авторства документов, обрабатываемых в электронной форме с помощью вычислительной техники.

Цифровая подпись жестко увязывает в одно целое содержание документа и секретный ключ подписывающего и делает невозможным изменение документа без нарушения подлинности данной подписи.

2. Процедура электронной подписи включает в себя два алгоритма: формирования цифровой подписи и проверки подлинности подписи.

Формирование подписи состоит в вычислении по документу, представленному в электронной форме, и секретному параметру(ключу подписывания), имеющемуся лишь у автора подписи, длинной цифровой последовательности, называемой цифровой подписью данного лица под данным документом.

Проверка подписи под документом состоит в осуществлении вычислений над содержимым документа, цифровой подписью под ними, "образцом подписи" лица, его подписавшего, результатом которых является признание или отрицание подлинности подписи данного лица под предъявленным документом.

Образец подписи - длинная цифровая последовательность(не являющаяся секретной),однозначно связанная с секретным ключом подписывания.

Главные требования к этим алгоритмам заключаются в исключении возможности получения подписи без использо­вания секретного ключа и гарантировании возможности про­верки подписи без знания какой-либо секретной информации.

Надежность схемы цифровой подписи определяется сложностью следующих трех задач:

— подделки подписи, то есть нахождения значения подпи-си под заданным документом лицом, не являющимся вла-дельцем секретного ключа;

— создания подписанного сообщения, то есть нахождения хотя бы одного сообщения с правильным значением подписи;

— подмены сообщения, то есть подбора двух различных сообщений с одинаковыми значениями подписи.

Для алгоритма проверки подписи необходима дополни-тельная открытая информация, связанная с обеспечением возможности открытой проверки подписи и зависящая от секретного ключа автора подписи. Эту информацию можно назвать открытым ключом цифровой подписи. Для исключения возможности подделки этой информации (открытого ключа) лицами, которые хотят выступить от лица законного владель-ца подписи (секретного ключа), создается инфраструктура состоящая из центров сертификации открытых ключей и обеспечивающая возможность своевременного подтверждения достоверности принадлежности данной открытой ин­формации заявленному владельцу и обнаружения подлога.

Цифровые подписи на основе шифрсистем с открытыми ключами

Идея использования систем шифрования с открытыми ключами для построения систем цифровой подписи как бы заложена в постановке задачи. Действительно, пусть имеется пара преобразований (Е, D), первое из которых зависит от открытого ключа, а второе — от секретного. Для того чтобы вычислить цифровую подпись S для сообщения, владелец секретного ключа может применить к сообщению Μ второе преобразование D: S = D(M). В таком случае вычислить подпись может только владелец секретного ключа, в то время как проверить равенство E(S) = Μ может каждый. Основ­ными требованиями к преобразованиям Ε и D являются:

— выполнение равенства Μ = E(D(M)) для всех сооб­щений М;

— невозможность вычисления значения D(M) для задан­ного сообщения Μ без знания секретного ключа.

Отличительной особенностью предложенного способа построения цифровой подписи является возможность отка­заться от передачи самого подписываемого сообщения М, так как его можно восстановить по значению подписи. В связи с этим подобные системы называют схемами цифровой подписи с восстановлением текста.