Деревья. Остов графа. Цикловой базис графа

Определение: Связный граф без циклов называется деревом.

Примеры:

Определение: Граф G, все компоненты связности которого являются деревьями, называют лесом.

Свойства деревьев:

Если граф G – дерево, то:

1) G – связный;

2) G не имеет простых циклов;

3) Если G имеет n вершин, то ребер (n-1);

4) Если у дерева G есть, по крайней мере, одно ребро, то у него обязательно найдётся висячая вершина;

5) Любые две различные вершины графа G можно соединить единственной простой цепью;

6) При добавлении к дереву любого нового графа получаем ровно один и притом простой цикл, который проходит через добавленное ребро.

При решении прикладных задач часто возникает необходимость обхода вершин графа, связанная с поиском вершин, удовлетворяющих определенным свойствам. Тогда если граф есть дерево, то его удобно изображать следующим образом. Выберем в дереве произвольную вершину α₀ и назовем её корнем дерева (или вершина нулевого яруса). Смежные с α₀ вершины назовем вершинами 1-го яруса и т.д.

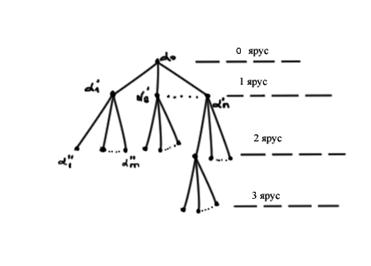
Номер яруса совпадает с расстоянием между его вершинами и корнем дерева.

Выделение корня в дереве определяет на множестве его вершин частичный порядок: .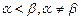

Корень ₀ является единственным минимальным элементом в этом частичном упорядоченном множестве вершин, а все концевые вершины – максимальные элементы.

Определение: Остовграфа G (или остовное дерево, или каркас графа G) – любой подграф графа G, содержащий все вершины графа G и являющийся деревом.

Если в связном графе G будем последовательно удалять циклические ребра до тех пор, пока это возможно, т.е. пока не останется ни одного циклического ребра, то мы придем к связному подграфу графа G с тем же множеством вершин, но без элементарных циклов, т.е. к дереву (остову).

Остов выбирается, вообще говоря, неоднозначно, в него входят все ациклические ребра.

Пусть G – граф, Д – его остов. Тогда все ребра подграфа G\Д называются хордами. Каждая хорда связывает две вершины остова.

На практике удобнее строить остов графа G путем последовательного удаления из G циклических ребер (хорд).

Пусть дан граф G=(V,X) v={v₁,…, v _n}, X={x₁,…,x_m}.

В остове графа G ребер будет (n-1) .

Тогда из графа G при построении остова удаляется m-(n-1)=m-n+1 ребер, т.е. m-n+1 – количество хорд (количество удаленных циклических ребер).

Определение: Число m-n+1 называется цикломатическимчислом связного графа G и обозначается v(G) (или циклическим рангом).

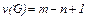
Определение: Независимая система циклов { ₁,…, _n} называется цикловымбазисом мультиграфа G, любой цикл из графа G является линейной комбинацией циклов этой системы.

Утверждение: Если мультиграф G не является ациклическим, то в нём существует цикловой базис, элементами которого являются простые циклы.

Теорема: Количество элементов в цикловом базисе мультиграфа G=(V,X) совпадает с его цикломатическим числом. То есть цикломатическое число показывает, чему равна размерность пространства базисов циклов графа.

Для несвязного графа с к компонентами связности базис циклов графа получается объединением базисов его связных компонент.

Утверждение 1: Неорграф G является лесом тогда и только тогда, когда υ(G)=0.

Утверждение 2: Неорграф G имеет единственный цикл тогда и только тогда, когда υ(G)=1.