Упражнения. 10.1. Найти хроматические числа для графов:

10.1. Найти хроматические числа для графов:

а) К₆

б) К_3,5

в) Е²

г) Е³

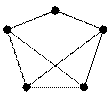
10.2. Найти независимые множества вершин, вершинное число независимости и хроматическое число графа G:

а) б) в)

10.3. Найти хроматическое число графа, заданного матрицей смежности:

10.4. Используя точный алгоритм раскрашивания, раскрасить вершины графов из задач 10.2, 10.3.

10.5. Построить граф с хроматическим числом, равным:

а) 4

б) 5

в) 3.

10.6. Найти толщину графа:

варианты контрольных работ

Часть 1. Элементы теории множеств и отношений

Вариант № 1.

1. Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: A´(BÈC)=(A´B)È (A´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и y<3x+8}.

4. Проверить, какими свойствами обладает бинарное отношение

={((a,b),(c,d)) | a+d=b+c}, заданное на множестве N´N.

5. Задать некоторое разбиение множества А={1,3,5,7,9}. Записать отношение эквивалентности, соответствующее данному разбиению. Найти фактор-множество множества А.

Вариант № 2.

1. Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: (AÈB)´C=(A´C)È (B´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и y=x³}.

4. Проверить, какими свойствами обладает бинарное отношение

={(А, В) / точки А и В лежат по одну сторону от заданной прямой}, заданное на множестве всех точек плоскости.

5. На множестве А={1,3,5,7,9} задано отношение эквивалентности

={(1, 1), (3, 3), (5, 5), (7, 7), (9, 9), (1, 3), (3, 1)}. Найти классы эквивалентности, порожденные элементами данного множества.

Вариант № 3.

1.Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: A´(B\C)=(A´B)\(A´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и 2x+y<7}.

4. Проверить, какими свойствами обладает бинарное отношение

={((a,b),(c,d)) | ad=bc} заданное на множестве N´N.

5. На множестве А={1,3,5,7,9} задано отношение эквивалентности

={(1, 1), (3, 3), (5, 5), (7, 7), (9, 9), (1, 3), (3, 1)}. Найти фактор-множество множества А.

Вариант № 4.

1. Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: A´(BÇC)=(A´B)Ç(A´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и x²+y²>8}.

4. Проверить, какими свойствами обладает бинарное отношение

={(x,y)| окружность y пересекает окружность x или совпадает с ней}, заданное на множестве всех окружностей плоскости.

5. На множестве А={1,3,5,7,9} задать минимальное отношение эквивалентности. Найти классы эквивалентности и фактор-множество множества А.

Вариант № 5.

1. Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: (AÇB)´C=(A´C)Ç(B´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и 3x≥5y}.

4. Проверить, какими свойствами обладает бинарное отношение

={((a,b),(c,d)) | a/c=b/d}, заданное на множестве N´N.

5. Задать некоторое разбиение множества А={2, 3, 4, 5, 7}. Записать отношение эквивалентности, соответствующее данному разбиению. Найти фактор-множество множества А.

Вариант № 6.

1. Упростить запись множества, используя основные равенства множеств:

.

2. Доказать тождество: (A \ B)´C=(A´C) (B´C).

3. Найти область определения, область значений бинарного отношения , инверсию бинарного отношения и композиции ◦ , ◦ ^-1, ^-1◦ , если ={(x,y) | x,y R и x²+y²<3}.

4. Проверить, какими свойствами обладает бинарное отношение

={(x,y)| общая часть треугольников x и y есть треугольник}, заданное на множестве всех треугольников плоскости.

5. На множестве А={1,3,5,7,9} задано отношение эквивалентности

={(1,1),(3,3),(5,5),(7,7),(9,9)}. Найти классы эквивалентности, порожденные элементами данного множества и фактор-множество множества А.