
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Часть 1. 1.5. а) AÈB=[-5; 8]; AÇB=[0; 1]; A\B=(1; 8]; B\A=[-5; 0);
§ 1
1.5. а) AÈB=[-5; 8]; AÇB=[0; 1]; A\B=(1; 8]; B\A=[-5; 0);
A+B=[-5; 0)Ç(1; 8];
б) AÈB =(-¥; +¥); AÇB =[0; 5]; A\B=(-¥; 0); B\A=(5; +¥);
A+B=(-¥;0)Ç(5;+¥);
в) AÇB=А; AÈB=N; A\B=Æ; B\A={x|x=2k–1; kÎN};
A+B=B\A;
г) AÇB=A; AÈB=B; A\B=Æ; B\A={0}; A+B={0}.
1.6. (-1;3)
1.9. 140
1.10. 20
1.12. 100
1.13. а) (AÇB) ÈC; б)  в)
в) 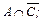 г)
г)  д)
д) 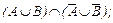
§ 2
2.4. а) Дr={1,3,5,7} Rr={3,5,7}
r-1={(3,7), (7,3), (3,5), (5,1)}
ror={(3,3), (7,7), (5,7), (1,3)}
ror-1={(3,3), (7,7), (7,5), (5,7), (5,5); (1,1)}
r-1or={(3,3), (7,7), (5,5)}
r-1or-1={(3,3), (7,7), (7,5), (3,1)}
в) Дr=R, Rr=R, r-1=r
ror={(x,y)/x,yÎR}
г) Дr={x/x=2n-1, nÎN}
Rr={y/y=2n-1, nÎN}
r-1=r, ror=r
д) Дr=R, Rr=R
r-1={(x,y)/x,yÎR и x<2y-1}
ror={(x,y)/x,yÎR и y<4x-3}
r-1or=ror-1={(x,y)/x,yÎR}
r-1or-1={(x,y)/x,yÎR и x<4y-3}
e) Дr=R, Rr=R
r-1={(x,y)/x,yÎR и x=y2}
ror={(x,y)/x,yÎR и y=x4}
ror-1={(x,y)/x,yÎR и x2=y2}
r-1or={(x,y)|x,yÎR и x=y}
r-1or-1={(x,y)|x,yÎR и x=y4}
§ 3
3.1. а) нерефлексивное, несимметричное, нетранзитивное отношение;
б) рефлексивное, симметричное, транзитивное отношение;
в) рефлексивное, симметричное, транзитивное отношение;
г) антирефлексивное, антисимметричное, транзитивное отношение;
д) нерефлексивное, симметричное, транзитивное отношение;
е) рефлексивное, антисимметричное, транзитивное отношение;
ж) рефлексивное, симметричное, транзитивное отношение;
з) рефлексивное, симметричное, транзитивное отношение.
3.2. а) r={(4,4), (6,6), (4,6), (6,4), (-2,-2), (0,0), (-2,0), (0,-2), (3,3)};
б) r={(4,4), (6,6), (-2,-2), (0,0), (6,-2), (-2,6), (6,0), (0,6), (-2,0),
(0,-2), (3,3)}
3.3. а) [2]r1= {2}; [4]r1= {4}; [6]r1= {6}; [8]r1= {8}
A/r1= {{2}, {4}, {6}, {8}};
б) [2]r2= {2, 4}; [4]r2= {2, 4}; [6]r2= {6}; [8]r2= {8}
A/r2= {{2, 4}, {6}, {8}};
в) [2]r3= {2, 4}; [4]r3= {2, 4}; [6]r3=[8]r3= {6, 8}
A/r3= {{2, 4}, {6, 8}}
§ 4
4.1. а) отношение частичного нелинейного порядка;
б) отношение строгого нелинейного порядка;
в) отношение частичного нелинейного порядка;
г) не является отношением порядка;
д) отношение строгого линейного порядка.
r={ (a,a), (b,с) (а,b), (b,b) (c,c), (a,c) };
r – отношение строгого порядка на множестве А.
r1={(a,b), (a,c), (a,d), (b,d), (c,d) (b,c)};
отношение строгого линейного порядка.
§ 5
5.1. а) функция;
б) не является функцией;
в) не является функцией;
г) функция;
д) не является функцией;
е) не является функцией;
ж) не является функцией;
з) функция;
и) не является функцией;
к) функция.
5.2. а) f – не инъективное, не сюръективное; g – не инъективное, сюръективное;
б) f – инъективное, не сюръективное;
в) f – инъективное, не сюръективное;
г) f – не инъективное, сюръективное;
д) f – биективное;
е) f – не инъективное, не сюръективное.
Дата добавления: 2015-01-29; просмотров: 366; Мы поможем в написании вашей работы!; Нарушение авторских прав |