
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Эйлеровы цепи и циклы в графах. Эйлеровы графы. Гамильтоновы цепи и циклы в графах. Гамильтоновы графы
Определение: Эйлеровацепь в графе – это цепь, содержащая все ребра графа, причем через каждое ребро проходим ровно один раз.
Определение: Эйлеровцикл в графе – цикл, содержащий все ребра графа, причем через каждое ребро проходим ровно один раз.
Определение: Граф, обладающий эйлеровым циклом, называется эйлеровымграфом.
Необходимое условие существования эйлерова цикла и эйлеровой цепи – связность графа.
Теорема(необходимое и достаточное условия существования эйлерова цикла): Связный неориентированный псевдограф тогда и только тогда является эйлеровым (т. е. обладает эйлеровым циклом), когда степень каждой его вершины есть четное число.
Теорема (необходимое и достаточное условия существования эйлеровой цепи): Связный неориентированный псевдограф обладает эйлеровой цепью тогда и только тогда, когда он имеет ровно две вершины нечетной степени.
Замечание: Если в графе G эйлерова цепь существует, то она цепь соединяет вершины нечетной степени.
Рассмотрим задачу построения алгоритма выделения эйлеровой цепи или эйлерова цикла в псевдографе.
Утверждение 1: Пусть G = (V, X) – связный псевдограф.  1,…,
1,…,  l циклы в графе G (l >1) и X(
l циклы в графе G (l >1) и X(  1)
1) 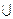 …
… 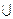 X(
X(  l) = X
l) = X
X(  i) ∩ X(
i) ∩ X(  j) = Ø при i ≠ j. Тогда для цикла
j) = Ø при i ≠ j. Тогда для цикла  1 найдется цикл
1 найдется цикл  i(i ≠ 1), такой, что V(
i(i ≠ 1), такой, что V(  1) ∩ V(
1) ∩ V(  i)
i) 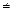 Ø.
Ø.
Утверждение 2: Если G=(V,X) – связный псевдограф, не содержащий висячих вершин, то в графе G существует хотя бы один цикл.
Алгоритм выделения эйлерова цикла в связном мультиграфе (алгоритм Флери):
Пусть G = (V, X), X 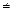 Ø и степени всех вершин четные.
Ø и степени всех вершин четные.
Шаг 1: Выделим из графа G цикл  1. (Такой цикл существует по утверждению 2).Пусть l = 1, G’ = G.
1. (Такой цикл существует по утверждению 2).Пусть l = 1, G’ = G.
Шаг 2: Удаляем из графа G’ ребра, принадлежащие множеству X(  l). Полученный псевдограф обозначаем снова через G’ (в G’ все вершины имеют четные степени). Если в G’ отсутствуют ребра, то переходим к шагу 4. В противном случае выделяем из G’ цикл и переходим к шагу 3.
l). Полученный псевдограф обозначаем снова через G’ (в G’ все вершины имеют четные степени). Если в G’ отсутствуют ребра, то переходим к шагу 4. В противном случае выделяем из G’ цикл и переходим к шагу 3.
Шаг 3: Присваиваем l:= l + 1 и переходим к шагу 2.
Шаг 4: По построению  1,…,
1,…,  l – циклы, удовлетворяющие условию утверждения 1. Если l = 1, то
l – циклы, удовлетворяющие условию утверждения 1. Если l = 1, то  1 – искомый эйлеров цикл, и на этом работа алгоритма заканчивается. В противном случае находим цикл
1 – искомый эйлеров цикл, и на этом работа алгоритма заканчивается. В противном случае находим цикл  i: V(
i: V(  1)∩ V(
1)∩ V(  i) ≠ Ø (2 ≤ i ≤l ). Переходим к шагу 5.
i) ≠ Ø (2 ≤ i ≤l ). Переходим к шагу 5.
Шаг 5: Присваиваем l: = l – 1
 1:=
1:=  1+
1+  i,
i,  j:=
j:=  j+1, j = i,…,l и переходим к шагу 4.
j+1, j = i,…,l и переходим к шагу 4.
Рассмотрим задачу о выделении эйлеровой цепи.
Пусть дан связный псевдограф G = (V, X), X ≠ Ø , имеющий ровно две вершины v и w нечетной степени. Добавим в G ребро (v,w), получим псевдограф G’ с четными степенями вершин. Выделим из G’ эйлеров цикл (по алгоритму) и удалим из него ребро (v,w). В результате получим эйлерову цепь, соединяющую v,w.
Определение: Гамильтоновцикл (цепь) – цикл (цепь), проходящий (проходящая) через каждую вершину графа в точности по одному разу.
Гамильтонов цикл (цепь) всегда является простым (простой). Он (она) может не содержать всех ребер графа.
Определение: Граф, обладающий гамильтоновым циклом, называется гамильтоновымграфом.
С понятием гамильтоновых циклов тесно связана так называемая задача коммивояжера: в нагруженном графе G определить гамильтонов цикл минимальной длины (иными словами, коммерсант должен совершить поездку по городам и вернуться обратно, побывав в каждом городе ровно один раз, и при этом стоимость такой поездки должна быть минимальной).
Математическая постановка задачи выглядит так: требуется найти гамильтонов цикл минимального веса.
На первый взгляд, понятие «гамильтонов цикл» сходно с понятием эйлерова цикла.
Пример:

– существуют гамильтонов и эйлеров циклы

 – не существует эйлерова цикла, существует гамильтонов цикл.
– не существует эйлерова цикла, существует гамильтонов цикл.
– существует эйлеров цикл, но не существует гамильтонова цикла.

– не существует эйлерова цикла и не существует гамильтонова цикла.
Данные примеры показывают независимость понятий гамильтонова и эйлерова циклов.
Несмотря на схожесть задач о нахождении этих циклов, решение о нахождении гамильтонова цикла значительно сложнее. Известны следующие достаточные условия существования гамильтоновых циклов в связном неорграфе G без петель, имеющем n  3 вершин:
3 вершин:
полнота графа (если граф полный, то он гамильтонов);
если для любых двух различных несмежных вершин vi, vj (i  j) графа G выполняется условие δ(vi) + δ(vj)
j) графа G выполняется условие δ(vi) + δ(vj)  n, то существует гамильтонов цикл;
n, то существует гамильтонов цикл;
если для любой вершины v графа G выполнено условие δ(v)  n/2, то существует гамильтонов цикл.
n/2, то существует гамильтонов цикл.
Необходимое условие существования гамильтонова цикла – связность графа и отсутствие точек сочленения.
Дата добавления: 2015-01-29; просмотров: 2376; Мы поможем в написании вашей работы!; Нарушение авторских прав |