Упражнения. 4.1. Найти число ребер и степени вершин в полных графах К6, К7, К8.

4.1. Найти число ребер и степени вершин в полных графах К₆, К₇, К₈.

4.2. Найти количество ребер в полных двудольных графах К_{4, 6}, К_{3, 5}, К_{2, 3}. Составить матрицу связности графа К_{2, 3}.

4.3. Найти количество ребер в графах Е², Е³, Е⁴. Построить реализации графов Е², Е³ (Е², Е³, Е⁴ – двух-, трех-, четырехмерные кубы).

4.4. Найти число полных трехвершинных подграфов в полных двудольных графах К_{3, 5}, К_{4, 3}.

4.5. Количество ребер в однородном графе G равно 15. Степень каждой вершины графа равна 3. Найти количество вершин графа G.

4.6. Существует ли полный граф с семью ребрами? С 50 ребрами?

4.7. Дан полный граф G и "_i: δ (v _i) = 20. Найти количество вершин и ребер графа.

4.8. Доказать, что графы Е³, Е⁴ являются двудольными.

4.9. Найти дополнение графа G до полного графа. Составить матрицы смежности графа G и его дополнения (по формуле).

G:

4.10. Для заданного графа G:

а) Построить соответствующий реберный граф;

б) Найти матрицу смежности реберного графа через матрицу инцидентности исходного графа (по формуле);

в) Определить степени вершин реберного графа через степени вершин исходного графа;

г) Определить число ребер в реберном графе, используя исходный граф G:

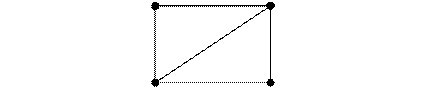
4.11. Построить однородный 5-вершинный граф. Составить его матрицу инцидентности. По матрице инцидентности найти матрицу смежности однородного графа. Построить соответствующий реберный граф. Найти его матрицу смежности, степени вершин, число ребер, используя исходный однородный граф.

§ 5. Поиск путей (маршрутов) с минимальным числом дуг (ребер)

Определение: Путь (маршрут) в орграфе Д (графе G) из вершины v_i в вершину v_j (i j) называется минимальным, если он имеет минимальную длину среди всех путей (маршрутов) орграфа Д (графа G).

Алгоритм поиска минимального пути из v в w орграфе Д (графе G).

Введем обозначения: Пусть Д = (V, X) – орграф, v V, V₁ V

Обозначим

Д(v) = {w V | (v,w) X} – образ вершины v

Д^-1(v) = {w V | (w, v) X} – прообраз вершины v

Д(V₁) = Д(v), где v V₁ – образ множества вершин V₁.

Д^-1(V₁) = 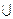Д^-1(v), где v V₁ – прообраз множества вершин V₁.

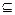Пусть G = (V, X) – граф, v V, V₁ V

Обозначим

G(v) = {w V | (v,w) X} – образ вершины v

G(V₁) = 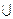G(v), где v V₁ – образ множества вершин V₁

Пусть Д = (V, X) – орграф с n вершинами (n 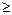2).

v, w – заданные вершины из V, v 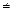w.

Опишем алгоритм поиска минимального пути из v в w в орграфе Д (алгоритм фронта волны).

1. Помечаем вершину v индексом 0, т. е. F W₀ (v) = { v }. Затем помечаем образы вершины v, индексом 1. Множество вершин с индексом 1 обозначим FW₁(v). Полагаем k = 1.

2. Если FW_k(v) = Ø или k = n – 1, w FW_k(v), то вершина w не достижима из вершины v, и работа алгоритма на этом заканчивается. В противном случае переходим к шагу 3.

3. Если w FW_k(v), то переходим к шагу 4. В противном случае существует путь из v в w длины k и этот путь минимальный.

Последовательность вершин:

v w₁ w₂ … w_k-1w, где

w_k-1 F W_k-1 (v) ∩ Д^-1 (w) (1)

w_k-2 F W_k-2 (v) ∩ Д^-1 (w_k-1)

…

w₁ F W₁ (v) ∩ Д^-1 (w₂)

и есть искомый путь длины k из v в w. На этом работа алгоритма заканчивается.

4. Помечаем индексом k+1 все непомеченные вершины, которые принадлежат образу множества вершин с индексом k. Множество вершин с индексом k+1 обозначаем F W_k+1 (v). Присваиваем k := k+1 и переходим к шагу 2.

Множество F W(v) в алгоритме обычно называют фронтом волны
k-гоуровня.

Вершины w₁, …, w_k-1 из последовательности (1), вообще говоря, могут быть выделены неоднозначно. Эта неоднозначность соответствует случаям, когда существует несколько различных минимальных путей из v в w.