Определение: Замкнутый маршрут (путь), в котором все ребра (дуги) попарно различны, называется циклом (контуром).

Определение: Цикл (контур), в котором все вершины попарно различны, называется простымциклом (простымконтуром).

Определение: Неориентированный граф без циклов называется ациклическим.

Определение: Орграф, не имеющий контуров, называется бесконтурным.

Определение: Вершина v называется достижимой из вершины u, если существует маршрут, связывающий вершины u и v.

Способы задания графов. Матричное задание графов.

Существует несколько способов задания графов:

1. Перечисление (список) ребер графа и вершин графа.

2. В виде геометрического объекта (реализация).

3. Матричный способ

а) матрица смежности А;

б) матрица инцидентности В.

Пусть Д=(V, X) – орграф, где V={v₁, …, v_n}, X={x₁, …, x_m}

Определение: Матрицейсмежностиорграфа Д называется квадратная матрица A(Д)= [a_ij] порядка n, у которой

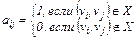
Определение: Матрицейинцидентности(илиматрицей инциденций) орграфа Д называется матрица B(Д)=[в_ij] размерности n x m, у которой

Пусть G=(V, X) – неориентированный граф, где V={v₁, …, v_n},
X={x₁, …, x_m}

Определение: Матрицейсмежностиграфа G называется квадратная матрица A(G)=[a_ij] порядка n, у которой

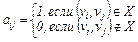
Определение: Матрицейинцидентностиграфа G называется матрица B(G)=[в_ij] размерности n x m, у которой

Замечание: Матрицу смежности можно определить и для псевдографов. Тогда в случае ориентированного (неориентированного) псевдографа a_ij=k , где k – кратность дуги (ребра) (v_i,v_j) в этом псевдографе. Определение матрицы инцидентности без изменений переносится и на произвольные мультиграфы (ориентированные и неориентированные) и на неориентированные псевдографы; только в случае петли (v_i, v_i) ставим в матрице инцидентности α.

Матрица A(G) является симметричной для любого неориентированного графа G.

Матрица A(Д), где Д – орграф, в общем случае симметричной не является.

По матрице смежности графа (орграфа) всегда можно определить ребра графа (дуги орграфа) как пары инцидентных им вершин, а для псевдографов, кроме того, и кратность ребер (дуг).

Однако, если рёбра (дуги) были пронумерованы, то восстановить их номера по матрице смежности невозможно.

В этом случае более информативной оказывается матрица инцидентности.