Определение: Вершина, инцидентная ровно одному ребру, и само ребро называются концевыми (иливисячими).

Определение: Степеньювершины vграфа G называется число 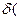v), равное числу ребер, инцидентных вершине v.

У изолированной вершины 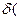v) = 0.

У висячей вершины 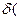v) = 1.

Определение: Полустепеньюисхода вершины v в орграфе Дназывается число 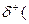v), равное количеству дуг, исходящих из вершины v.

Определение: Полустепеньюзахода вершины v в орграфе Д называется число 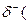v), равное количеству дуг, заходящих в вершину v.

Кол-во вершин и ребер в графе G будем обозначать соответственно n(G) и m(G). Кол-во вершин и дуг в орграфе Д будем обозначать соответственно n(Д) и m(Д).

Утверждение 1. Для любого псевдографа G выполняется равенство:

.

Утверждение 2. Для любого ориентированного псевдографа Д выполняется равенство:

.

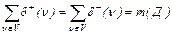Определение: Подграфом графа G называется граф, все вершины и рёбра которого содержатся среди вершин и ребер графа G.

Определение: Подграфназывается собственным, если он отличен от самого графа.

Определение: Объединением графов G₁=(V₁, X₁) и G₂=(V₂, X₂) называется граф G=G₁+G₂=(V₁ 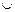V₂, X₁ 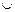X₂).

Определение: Пересечением графов G₁=(V₁, X₁) и G₂=(V₂, X₂), где V₁ V₂ 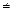0, называется граф G=G₁ 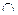G₂=(V₁ 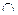V₂, X₁ 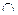X₂).

Определение: Произведением графов G₁=(V₁, X₁) и G₂=(V₂, X₂) называется граф G=G₁×G₂=(V, X), для которого V=V₁×V₂ – декартово произведение множеств вершин исходных графов, а множество ребер X определяется следующим образом: вершины (u₁, u ₂) и (v₁, v₂) смежны в графе G тогда и только тогда, когда или u₁=v₁, а u₂ и v₂ смежны в графе G₂, или u₂=v₂, а u₁ и v₁ смежны в графе G₁.

Часто бывает важно определить, какие графы считаются различными, а какие не различаются. Обычно это связывают с понятием изоморфизма графов.

Определение: Два графа G₁=(V₁, X₁) и G₂=(V₂, X₂) называются изоморфными, если существуют взаимно однозначные отображения f и g, такие, что f: V₁ ® V₂ и g: X₁ ® X₂, сохраняющие инцидентность.

Обозначаются: G₁ ~ G₂.

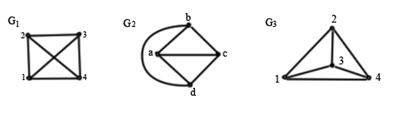Во многих случаях можно рассматривать графы с точностью до изоморфизма, т.е. не различать изоморфные графы. Однако, если какие-то вершины или рёбра графа обладают различной индивидуальностью, например, они занумерованы или им сопоставлены какие-либо численные характеристики (вес ребра, длина ребра и др.), то естественно при сравнении двух графов эту индивидуальность учитывать.

G₁~G₂~G₃

Определение: Последовательность вершин и ребер (дуг) графа G (орграфа Д) v₁x₁v₂x₂v₃…x_kv_k+1(k 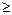1) называется маршрутом (путём) из вершины v₁ в вершину v_k+1.

Определение: Длина пути (маршрута) равна количеству дуг (ребер) в последовательности (=k).

Определение: Вершина v₁ называется началоммаршрута (пути), а v_{k+1 –} концом. Остальные вершины называются внутренними.

Маршрут (путь) рассматривается как непрерывная траектория движения по вершинам и рёбрам графа.

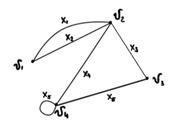
Пример: v₁x₁v₂x₃v₃x₆v₄ – маршрут из v₁ в v₄ длиной 3.

Определение: Незамкнутый маршрут (путь), в котором все рёбра (дуги) попарно различны, называется цепью.

Определение: Цепь, в которой все вершины попарно различны, называется простойцепью.