Упражнения. 5.1. Какие из следующих отношений являются функциями?

5.1. Какие из следующих отношений являются функциями?

а) r={(1, 2), (2, 3), (5, 7), (0, 4), (, Ñ), (*, Ñ)};

б) r={(1, 2), (2, 3), (5, 7), (0, 4), (, Ñ), (5, Ñ)};

в) r={(х, у) | х, уÎR, х делится на у};

г) r={(х, у) | х, уÎR, у=х³-1};

д) хrу, если прямая х параллельна прямой у (на множестве всех прямых плоскости);

е) хrу, если человек х преподаватель человека у (на некотором множестве людей);

ж) r={(х, у) | х, уÎR, (х-2)²+у²=5};

з) r={(х, 3|x|) | хÎR};

и) хrу, если прямая х перпендикулярна прямой у (на множестве всех прямых плоскости);

к) хrу, если у – количество букв в слове х (на множестве всех слов русского языка);

5.2. Установить вид следующих отображений:

а) А – множество слов русского языка, В – множество букв алфавита русского языка,

f – отображение, которое каждое слово из А отображает в его первую букву,

g – отображение, которое каждое слово из А отображает в его вторую букву.

б) f: Z®Z f(x)=2x+3;

в) f: R®R f(x)=е^х;

г) f: R®R f(x)=х³-х;

д) f: Z®Z f(x)=x+5;

е) f: R®R f(x)=хSinx

ж) f: R®R f(x)=х²

5.3. Пусть Х – конечное множество и отображение f: Х®Х инъективно. Доказать, что f биективно.

5.4. Доказать, что отображение f: X®Y имеет обратное отображение f^-1: Y®X тогда и только тогда, когда f – биекция.

5.5. Пусть f: А®В, где А и В – конечные множества, состоящие из n элементов каждое. Доказать, что:

а) если f инъективно, то f сюръективно;

б) если f сюръективно, то f инъективно.

Часть 2. Теория графов

Исторически сложилось так, что теория графов зародилась в ходе решения головоломок около трехсот лет назад.

Толчок к развитию теория графов получила на рубеже 19 и 20 столетий, когда резко возросло количество работ в области топологии и комбинаторики. Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы 20 столетия.

Графы используются в теории планирования и управления, в теории расписаний, в социологии, биологии, химии, медицине, в электронике, теории конечных автоматов и других областях знаний.

Основные понятия теории графов

Во многих прикладных задачах изучаются системы связей между различными объектами. Объекты отмечаются точками, а связи между вершинами отмечаются отрезками (стрелками) между соответствующими точками.

Такие системы и образуют графы. Точки – вершины графа. Отрезки – ребра графа.

Граф может изображать сеть улиц в городе: вершины графа – перекрестки, а дуги – улицы с разрешенным направлением движения (улицы могут быть с односторонним и двусторонним движением).

В виде графов можно представить блок-схемы программ (вершины – блоки, а дуги – разрешенные переходы от одного блока к другому), электрические цепи, географические карты, молекулы химических соединений и др.

Определение: Введем в рассмотрение два конечных множества.

V – непустое множество объектов V={v₁, …, v _n}

X – некоторый набор пар элементов из V вида x=(v, w) (которые связаны между собой)

Графом – называется алгебраическая система G= (V, X), где V – множество вершин графа, а X – множество ребер графа.

Пример:

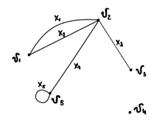
G= (V, X)

V={v₁, v₂, v₃, v₄, v₅}

X={( v₁, v₂), (v₁, v₂), (v₂, v₃), (v₂, v₅), (v₅, v₅)}

или

X={x₁, x₂, x₃, x₄, x₅}

Определение: Ребра вида (v, v) называются петлями.

Определение: Одинаковые ребра, т.е. соединяющие одни и те же вершины, называются кратными(или параллельными) ребрами.

Определение: Количество кратных ребер (u, v) называется кратностью ребра (u, v).

Определение: Псевдограф – граф с кратными ребрами и петлями.

Определение: Мультиграф –псевдограф без петель.

Определение: Вершины, не принадлежащие ни одному ребру, называются изолированными.

Определение: Если в графе G указано направление ребер, то граф называется ориентированным.

Для ориентированных графов будем использовать букву Д.

Ребра ориентированного графа называются дугами.

Определение: Если направление ребер не указано, то граф называется неориентированным (н-графом) или просто графом.

Если некоторому графу поставлена соответствующая геометрическая конфигурация, то данная конфигурация называется изображением (или реализацией) графа.

Определение: Если x= (u, v) – ребро графа, то вершины u и v называются концами ребра x.

Определение: Если x= (u, v) – дуга орграфа, то u называется началом, а v концом дуги x.

В этом случае говорят: что дуга x исходит из вершины u и заходит в вершину v.

Определение: Вершины u, v графа G=(V, X) (орграфа Д=(V, X)) называются смежными, если (u, v) Х, т. е. вершины u, v называются смежными, если существует ребро (дуга), соединяющая их.

Определение: Два ребра называются смежными, если они имеют общую вершину.

Определение: Если вершина v является концом (началом или концом) ребра (дуги) x, то говорят, что вершина v и ребро (дуга) x инциденты.