Отношения порядка

Определение:Бинарное отношение называется предпорядком(квазипорядком) на множестве А, если оно рефлексивно и транзитивно на множестве А.

Определение:Бинарное отношение называется отношениемчастичногопорядка на множестве А, если оно рефлексивно, транзитивно и антисимметрично на множестве А. Обозначение: .

Определение:Бинарное отношение называется отношениемстрогогопорядка на множестве А, если антирефлексивно, антисимметрично и транзитивно на множестве А. Обозначение: .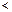

Определение:Отношение порядка на множестве А, для которого любые два элемента сравнимы, т.е. 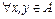: или , называется отношениемлинейногопорядка.

Определение:Множество А с заданным на нём частичным порядком называется частичноупорядоченныммножеством. Обозначение: .

Определение:Множество А с заданным на нём строгим порядком называется строгоупорядоченныммножеством. Обозначение: .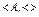

Определение:Элемент частично упорядоченного множества называется максимальным, если .

Определение:Элемент частично упорядоченного множества называется наибольшим, если . Обозначение: .

Определение:Элемент частично упорядоченного множества называется минимальным, если .

Определение:Элемент частично упорядоченного множества называется наименьшим, если . Обозначение: .

Всякое конечное частично упорядоченное множество содержит как максимальные, так и минимальные элементы (причём может не единственные). Наибольший и наименьший элементы частично упорядоченного множества (если они существуют) единственны.

Заметим, что всякий наибольший элемент является максимальным, а всякий наименьший элемент является минимальным. Обратные утверждения, вообще говоря, неверны.

Рассмотрим упорядоченное множество А с введённым на нём отношением порядка . Говорят, что элемент y покрывает элемент x, если и не существует такого элемента 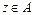, что и .

Если множество А конечно, то упорядоченное множество можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости, и если y покрывает x, то точки x и y соединяют отрезком, причём точку, соответствующую x, располагают ниже. Такие схемы называют диаграммами Хассе.