Понятие множества. Операции над множествами

Под множеством будем понимать совокупность определённых и различимых между собой объектов, которая рассматривается как единое целое. Эти объекты называются элементами множества.

Понятие множества принимается как исходное, первичное, т.е. не сводимое к другим понятиям. Множества будем обозначать большими буквами латинского алфавита: A, B, C… , а элементы множества – малыми буквами: a, b, c… .

Определение:Множество, не содержащее ни одного элемента, называется пустыммножеством. Обозначается символом .

Определение:Некоторое фиксированное множество, которое содержит все рассмотренные в данной теории множества, называется универсальными обозначается U.

Определение:Два множества A и B называются равными и обозначаются A=B, если A и B содержат одни и те же элементы, т.е. если каждый элемент множества A является элементом множества B, и каждый элемент множества B является элементом множества A.

Определение:Множество A называется подмножеством множества B, если каждый элемент множества A принадлежит множеству B. В этом случае пишут 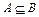. Символ 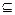называется знаком включения. Есл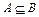и и , то говорят, что A есть собственное подмножество множества B. В этом случае пишут .

Множество всех подмножеств множества A называется множеством-степенью и обозначается P(A).

Для доказательства равенства двух множеств A и B достаточно доказать, что 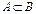и , т.е. доказательство равенства двух множеств состоит из доказательства двух утверждений:

1.

2.

Для графического изображения множеств и их свойств, а также отношений между ними используются так называемые диаграммы Эйлера-Венна. Множество изображается кругом (или другой связной фигурой) на плоскости и мыслится как множество точек круга (фигуры).