Полные графы. Двудольные графы. Однородные и реберные графы

Определение: Граф называется полным, если любые две различные вершины его соединены одним и только одним ребром (или если любые его две вершины смежны).

Полный неориентированный граф с n вершинами обозначается K_n.

Граф G, не являющийся полным, можно преобразовать в полный с теми же вершинами, добавив недостающие ребра. Вершины графа G и ребра, которые добавлены, также образуют граф. Он называется дополнением графа G до полного графа.

Определение: Дополнением графа G называется граф с теми же вершинами, что и граф G и теми ребрами, которые необходимо добавить графу G, чтобы получился полный граф.

Пример:

G:

Матрица смежности дополнительного графанаходится по формуле:

A ( ) = J – A (G)

где J – матрица смежности полного графа, состоящая полностью из единиц, за исключением элементов диагонали.

Определение: Двудольнымграфом G = (V, X) называется граф, вершины которого разбиты на два пересекающихся класса, т. е.: V = V₁ 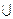V₂, V₁∩V₂ = Ø, а ребра связывают вершины только из разных классов – не обязательно все пары.

Определение: Если в двудольном графе каждая из вершин класса V₁ связана с каждой из вершин класса V₂, то граф называется полным двудольным и обозначается K_m,n , где m – количество вершин первого класса (множество V₁), n – количество вершин второго класса (V₂). Граф K_m,n содержит (m + n) вершин и m·n ребер.

К_3,2 K_3,3 Двудольный

Определение: Пусть G = (V, X) V = {v₁,v₂…,v_n}. Если вершины графа имеют одинаковую степень δ(v_i) = s для всех i { 1, 2, …, n}, то такой граф называется однородным(регулярным).

Теорема 1: Пусть дан однородный граф G = (V, X), V = {v₁,v₂…,v_n}, тогда:

δ(v_i) = n·s;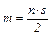

где n – количество вершин; m – количество ребер; s – степень каждой вершины.

Полный граф является однородным.

Теорема 2: Степень каждой вершины полного графа K_n на 1 меньше числа вершин, т. е. s = n – 1

Теорема 3: Если полный граф имеет n вершин, то

Для однородного графа G матрицы смежности и инцидентности связаны соотношением:

A(G) = B(G)· B^T(G) – s·E, где

B^T(G) – транспонированная матрица инцидентности B(G);

s – степень вершины v однородного графа;

Е – единичная матрица.

Определение: Граф G_p называется реберным, если в качестве вершин его выбраны ребра исходного графа G с m ребрами и n вершинами, имеющего матрицу инцидентности B(G).

В этом случае матрица смежности реберного графа находится по формуле: A (G_p) = B^T(G) · B(G) – 2E

Исходный граф G для построения реберного графа G_p необязательно должен быть регулярным. Если все же граф G является регулярным, то и реберный G_p тоже будет регулярным. В общем случае, если ребро x_i в графе G ограничено вершинами v_j и v_k , степень которых равна δ(v_j) и δ(v_k) , то степень вершины x_iв реберном графе G_p определяется по формуле:

δ(x_i) = δ(v_j) + δ(v_k) – 2

Число ребер в реберном графе G_p определяется по формуле:

m’ = δ²(v_i) – m = δ(x_i)