Формальное описание системы.

Система определяется кортежем:

S = 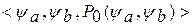, (1)

где 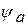- подмодель, определяющая поведение системы. Иногда эта подмодель может рассматриваться как «чёрный ящик», о котором известно только то, что на определённые воздействия он реагирует определённым образом;

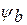- это подмодель, определяющая структуру системы, при её внутреннем рассмотрении;

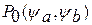- предикат целостности, определяющий назначение системы, семантику моделей , , и семантику преобразования 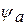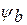, 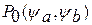=1, если преобразование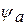 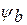существует.

Подмодель 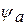может быть представлена в виде кортежа:

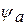=<x, y, z, f, g>, (2)

где x=x(t) – входной сигнал,

y=y(t) – выходной сигнал,

z=z(t) – переменная состояний модели ,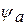

f, g – функционалы (глобальные уравнения системы), задающие текущие значения выходного сигнала y(t) и внутреннего состояния z(t).

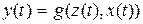, (3)

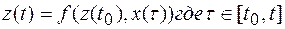, (4)

Выражение (3) называют уравнением наблюдения, а выражение (4) -уравнением состояния системы соответственно. Если в описание системы введены функционалы f и g, то она уже не рассматривается как «чёрный ящик». Однако для многих систем определение глобальных уравнений является затруднительным или даже невозможным.

Кроме выражения (1) систему задают следующими аксиомами:

· Для системы определены пространство состояний Z, в которых может находиться система, и параметрическое пространство Т, в котором задано поведение системы. В связи с этим описания вида (2) называют динамическими системами, так как они отражают способность системы изменять состояния z(t) в параметрическом пространстве Т. В отличие от динамических статические системы таким свойством не обладают. В качестве параметрического пространства рассматривается временной интервал (0, ).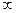

· Пространство состояний Z содержит не менее двух элементов.

· Система обладает свойством функциональной целостности, то есть она имеет свойства, которые нельзя свести к сумме свойств её элементов.

Дата добавления: 2015-02-09; просмотров: 18; Нарушение авторских прав