
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Этап 2. Синтез приоритетов
Это один из способов решения проблемы многокритериальности. Синтез приоритетов (СП) – это вычисление собственных векторов, которые после нормализации и являются векторами приоритетов. Собственные векторы искать сравнительно трудоемко, поэтому достаточно близкие оценки можно получить с помощью геометрического среднего, для чего элементы каждой строки перемножаются и из результата извлекается корень n-й степени.
Например, для Кр1 в матрице целей:
Кр1: 1*1/2*1/3*1/4*4*3 = ½ Þ  ,
,
Кр2: 2*1*1/2*1/3*1/4*1/4 = 0,0417 Þ  ,
,
Кр3: 3*2*1*1/3*1*1/2 = 1 Þ  ,
,
Кр4: 4*3*3*1*1*1/2 = 18 Þ  ,
,
Кр5: ¼*4*1*1*1*1 = 1 Þ  ,
,
Кр6: 1/3*4*2*2*1*1 = 16/3 Þ  .
.
Далее оценки нормируются путем деления на сумму  ;
;
α1 = 0,917 / 6,193 = 0,148; α4 = 1,435 / 6,193 = 0,23;
α2 = 0,616 / 6,193 = 0,1; α5 = 1 / 6,193 = 0,16;
α3 = 1 / 6,193 = 0,16; α6 = 1,23 / 6,193 = 0,198.
Полученные оценки – это матрица – строка приоритетов критериев α1х6 .
Далее для каждого из домов (альтернатив) рассчитываются приоритеты в смысле каждого из критериев:
Для критерия Кр1 получим:
для А:  ,
,
для В:  ,
,
для С:  ,
,
для D: 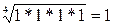 .
.
Сумма равна 0,76 + 1 + 1,56 + 1 = 4,32, поэтому нормированные значения приоритетов:
 .
.
Аналогично для остальных критериев получим
β21,… ,β24; β3,… ,β34; β41,… ,β44; β51,… ,β54; β61,… ,β64.
Данные приоритеты образуют матрицу В6х4.
Приоритеты альтернатив с учетом двух уровней, т.е. матриц α и В, получаются путем перемножения
Ц = αх В,
где Ц – матрица-строка глобальных приоритетов, т.е. оценки с точки зрения цели.
Дата добавления: 2015-02-09; просмотров: 343; Мы поможем в написании вашей работы!; Нарушение авторских прав |