
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Характеристики качества цифровых управляющих систем (ЦУС).
Качество ЦУС определяется временем пребывания заявок в системе, характеризуемым промежутком времени от момента поступления заявки и до момента окончания её обслуживания, в который заявка покидает систему.
Определение времени пребывания заявок – первоочередная задача анализа ЦУС.
Функционирование ЦУС рассматривается как совокупность трёх процессов: поступления заявок на вход системы, диспетчеризации и обслуживания заявок. Время пребывания заявок в системе зависит от характеристик каждого из этих процессов.
Моменты поступления заявок в ЦУС случайны. Время выполнения одной и той же программы, в общем, непостоянно и зависит от данных, поступающих извне. Таким образом, функционирование ЦУС носит стохастический характер, что позволяет рассматривать такие системы как системы массового обслуживания и описывать их в терминах теории массового обслуживания.
Потоки заявок на обслуживание.
Совокупность событий, распределённых во времени, называется потоком заявок.
t1 t2 t3 t4 t5 t6 t7 t8
 |
t1….tn – моменты времени возникновения событий, порождающих заявки.
Различают входящие и выходящие потоки заявок.
В общем случае поток заявок рассматривается как случайный процесс, задаваемый функцией распределения промежутков времени между моментами поступления двух соседних заявок.
Важнейшая характеристика потока - его интенсивность 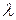 - среднее число заявок, поступающих в систему в единицу времени. Величина
- среднее число заявок, поступающих в систему в единицу времени. Величина  задаёт средний интервал времени между двумя соседними заявками.
задаёт средний интервал времени между двумя соседними заявками.
Поток заявок может быть стационарным и нестационарным.
· Стационарный, если его вероятностные характеристики не изменяются во времени
· Нестационарный в противном случае.
Характеристики ЦУС определяются наиболее просто для стационарного режима работы системы, предполагающего стационарность потоков заявок. Поэтому нестационарные потоки аппроксимируются на отдельных отрезках времени стационарными потоками.
Простейший поток.
В теории массового обслуживания наибольшее число результатов получено для простейшего потока.
Простейший поток – это поток, обладающий тремя свойствами:
1. стационарностью,
2. отсутствием последействия,
3. ординарностью.
Отсутствие последействия означает, что заявки поступают в систему независимо друг от друга. В частности, длина интервала времени до момента поступления следующей заявки не зависит от того, поступила ли заявка в начальный момент.
Ординарность означает, что в каждый момент времени в систему может поступить не больше одной заявки.
Для простейшего потока интервал времени между поступлением двух соседних заявок является случайной величиной с функцией распределения
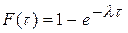 (1)
(1)
Распределение (1) называется показательным или экспоненциальным и имеет плотность распределения
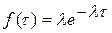 (2)
(2)
Математическое ожидание длины интервала времени между последовательными моментами поступления заявок

Дисперсия интервала времени между последовательными моментами поступления заявок :
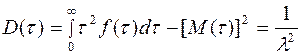
Вычислим вероятность появления коротких интервалов между двумя последовательными заявками, длина которых меньше мат. ожидания 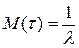 :
:
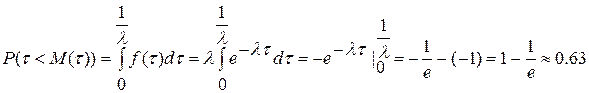 (3)
(3)
Таким образом, короткие интервалы более частые, чем длинные, т.е. при простейшем потоке создаются боле тяжёлые условия работы системы по сравнению с другими распределениями потоков заявок.
Для простейшего потока число заявок, поступающих в систему за интервал времени 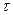 , распределено по закону Пуассона:
, распределено по закону Пуассона:
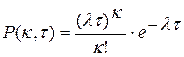 (
( 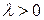 ), (4)
), (4)
где 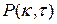 - вероятность того, что за время
- вероятность того, что за время 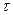 в систему поступит
в систему поступит 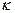 заявок,
заявок,
 - интенсивность потока заявок.
- интенсивность потока заявок.
Мат. ожидание и дисперсия распределения Пуассона:
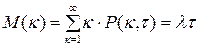

Нестационарный поток с интенсивностью  , который описывается законом распределения Пуассона, называется пуассоновским, но не простейшим, поскольку не выполняется свойство стационарности.
, который описывается законом распределения Пуассона, называется пуассоновским, но не простейшим, поскольку не выполняется свойство стационарности.
Простейший поток обладает следующими особенностями:
1. Сумма N независимых, стационарных, ординарных потоков с интенсивностями  i (I=1,…,N) сходится к простейшему потоку с интенсивностью
i (I=1,…,N) сходится к простейшему потоку с интенсивностью  при условии, что складываемые потоки оказывают более или менее одинаковое влияние на суммарный поток (т.е. сравнимы по интенсивности).
при условии, что складываемые потоки оказывают более или менее одинаковое влияние на суммарный поток (т.е. сравнимы по интенсивности).
Т.о. для выяснения свойств суммарного потока достаточно знать лишь интенсивности суммируемых потоков и не требуется знать внутреннюю структуру этих потоков.
Простейший поток обладает устойчивостью, состоящей в том, что при суммировании независимых простейших потоков получается простейший поток, при этом интенсивности складываемых потоков суммируются.
2. Поток заявок, полученный путём случайного разрежения исходного потока, когда каждая заявка с определённой вероятностью р исключается из потока независимо от того, исключены ли другие заявки, образует простейший поток с интенсивностью 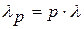 , где
, где 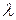 - интенсивность исходного потока. В отношении исходного потока заявок делается предположение лишь об ординарности и стационарности.
- интенсивность исходного потока. В отношении исходного потока заявок делается предположение лишь об ординарности и стационарности.
3. Так как простейший поток создаёт более сложный режим работы системы, то предположение о том, что на вход системы поступает простейший поток заявок, приводит к определению предельных характеристик качества обслуживания. Если реальный поток отличен от простейшего, то система будет функционировать не хуже, чем это следует из полученных оценок.
4. Интервал времени между произвольным моментом времени и моментом поступления очередной заявки имеет такое же распределение (1) с тем же средним  , что и интервал времени между двумя последовательными заявками. Эта особенность простейшего потока – следствие отсутствия последействия.
, что и интервал времени между двумя последовательными заявками. Эта особенность простейшего потока – следствие отсутствия последействия.
Длительность обслуживания заявок.
Длительность обслуживания заявки равна интервалу времени, необходимому прибору для обслуживания заявки. В общем случае это случайная величина с законом распределения B(τ) и математическим ожиданием  . Типы заявок различаются либо законами распределения, либо только средними значениями длительности обслуживания при одинаковых законах распределения. При этом предполагается независимость длительностей обслуживания для различных заявок одного типа, что справедливо для большинства реальных систем. Длительность обслуживания заявки процессором определяется временем выполнения соответствующей программы. В случае малой разветвленности программы, когда число выполняемых операций практически постоянно, длительность обслуживания может считаться постоянной и равной
. Типы заявок различаются либо законами распределения, либо только средними значениями длительности обслуживания при одинаковых законах распределения. При этом предполагается независимость длительностей обслуживания для различных заявок одного типа, что справедливо для большинства реальных систем. Длительность обслуживания заявки процессором определяется временем выполнения соответствующей программы. В случае малой разветвленности программы, когда число выполняемых операций практически постоянно, длительность обслуживания может считаться постоянной и равной  . В общем случае прикладные программы реализуют сложные алгоритмы с большим числом разветвлений. Количество операций, выполняемых в процессе обслуживания заявки, т.е. путь реализации алгоритма, определяется состоянием управляемого объекта, т.е. данными, поступающими в управляющую систему. При этом время выполнения программы рассматривается как случайная величина с математическим ожиданием
. В общем случае прикладные программы реализуют сложные алгоритмы с большим числом разветвлений. Количество операций, выполняемых в процессе обслуживания заявки, т.е. путь реализации алгоритма, определяется состоянием управляемого объекта, т.е. данными, поступающими в управляющую систему. При этом время выполнения программы рассматривается как случайная величина с математическим ожиданием  и дисперсией D. Если известно только среднее время θ* выполнения программы и отсутствуют сведения о законе распределения, то время выполнения программы целесообразно аппроксимировать экспоненциальным распределением следующего вида:
и дисперсией D. Если известно только среднее время θ* выполнения программы и отсутствуют сведения о законе распределения, то время выполнения программы целесообразно аппроксимировать экспоненциальным распределением следующего вида:
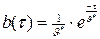 (5)
(5)
Аппроксимация (5) целесообразна по следующим причинам:
1. Использование экспоненциального распределения упрощает математическую модель.
2. Получаемые оценки являются предельными. Например, время обслуживания при других законах распределения, у которых коэффициенты вариации <1, оказывается не большим, чем при экспоненциальном распределении.
Экспоненциальное распределение длительности обслуживания имеет следующее свойство: интервал времени от любого случайного момента времени до момента окончания обслуживания заявки имеет то же экспоненциальное распределение с тем же средним, что и длительность обслуживания заявки.

 τ
τ


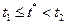
 t*
t*



t1 τ2 t2
t1 и t2 – моменты начала и окончания обслуживания, длительность которого τ. Тогда для случайного момента t* интервал времени 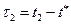 имеет тот же закон распределения, что и τ, т.е. закон распределения (5) со средним
имеет тот же закон распределения, что и τ, т.е. закон распределения (5) со средним  *.
*.
Отсюда следует, что при экспоненциальном законе распределения длительности обслуживания в случае прерывания обслуживания время дообслуживания заявки является случайной величиной с тем же законом распределения, что и длительность обслуживания, т.е. процессы обслуживания и дообслуживания протекают одинаково. Это свойство экспоненциального распределения является следствием отсутствия последействия, присущего всем процессам с экспоненциальным распределением интервалов времени.
Интенсивность обслуживания 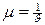 характеризует среднее количество заявок, которое может быть обслужено в единицу времени.
характеризует среднее количество заявок, которое может быть обслужено в единицу времени.
Лекция. Характеристики качества функционирования ЦУС.
Дата добавления: 2015-02-09; просмотров: 302; Мы поможем в написании вашей работы!; Нарушение авторских прав |