
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Преобразования Галилея. Механический принцип относительности
Из определения инерциальной системы отсчета (это та система отсчета, по отношению к которой выполняется закон инерции - первый закон Ньютона: материальная точка, на которую не действуют другие тела (изолированная точка), покоится, либо движется равномерно и прямолинейно) следует, что во всех инерциальных системах отсчета ускорение изолированной материальной точки должно быть равно нулю. Последнее позволяет установить, как должна двигаться относительно инерциальной системы отсчета какая-либо другая система, для того, чтобы она также была инерциальной. Оказывается, что две инерциальные системы отсчета могут двигаться друг относительно друга только поступательно и притом равномерно и прямолинейно.
 |
Рассмотрим две инерциальных системы отсчета: систему XYZ, которую будем условно считать неподвижной, и подвижную систему отсчета X/Y/Z/, скорость поступательного движения которой равна
 Примем для упрощения задачи, что в начальный момент времени t = 0 начала отсчета O и O’ обеих систем координат и соответствующие оси совпадали. В произвольный момент времени t ¹ 0 взаимное расположение этих систем имеет вид, изображенный на рис. 4.1. Скорость подвижной системы координат
Примем для упрощения задачи, что в начальный момент времени t = 0 начала отсчета O и O’ обеих систем координат и соответствующие оси совпадали. В произвольный момент времени t ¹ 0 взаимное расположение этих систем имеет вид, изображенный на рис. 4.1. Скорость подвижной системы координат 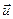 направлена вдоль прямой OO/, радиус-вектор, проведенный из O в O/, можно определить как:
направлена вдоль прямой OO/, радиус-вектор, проведенный из O в O/, можно определить как: 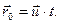
Положение произвольной точки М в неподвижной и подвижной системах отсчета определяются радиус-векторами 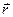 и
и  (см. рис. 4.1), причем
(см. рис. 4.1), причем
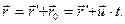
| (4.1.1,а) |
В проекциях на оси координат уравнение (4.1.1,а) можно записать в следующем виде:

| (4.1.1,б) |
В классической ньютоновской механике принимают, что ход времени не зависит от относительного движения системы отсчета. Поэтому систему уравнений (4.1.1,б) можно дополнить еще одним: t = t/. Выражения (4.1.1,а) и (4.1.1,б) называют преобразованием Галилея.
Дифференцируя уравнение (4.1.1,а) по времени, и учитывая, что  найдем соотношение между скоростями и ускорениями точки М относительно обеих систем:
найдем соотношение между скоростями и ускорениями точки М относительно обеих систем:
 
| (4.1.2) |
Первое уравнение в (4.1.2) называют законом сложения скоростей в классической механике. Если точка М не подвержена действию других тел, то  Так как
Так как  (из (4.1.2)), рассматриваемая нами подвижная система действительно является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
(из (4.1.2)), рассматриваемая нами подвижная система действительно является инерциальной – изолированная материальная точка либо движется относительно нее равномерно и прямолинейно, либо покоится.
В общем случае силы взаимодействия между телами зависят от взаимного расположения этих тел и от скорости их движения друг относительно друга. Из соотношений (4.1.1,а) и (4.1.2) следует, что для любых двух материальных точек 1 и 2 можно получить:  и
и 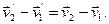 Следовательно, силы, действующие на данную материальную точку (или тело) со стороны других тел, одинаковы во всех инерциальных системах отсчета, то есть
Следовательно, силы, действующие на данную материальную точку (или тело) со стороны других тел, одинаковы во всех инерциальных системах отсчета, то есть

| (4.1.3) |
Из уравнений (4.1.2) и (4.1.3) для инерциальных систем отсчета получим, что  Таким образом, из приведенного выше материала следует, что инвариантами (инвариант – физическая величина, которая не зависит от выбора системы отсчета и является одинаковой во всех инерциальных системах) в механике Ньютона являются: 1) интервал времени (Dt = t2 – t1), 2) длина отрезка (
Таким образом, из приведенного выше материала следует, что инвариантами (инвариант – физическая величина, которая не зависит от выбора системы отсчета и является одинаковой во всех инерциальных системах) в механике Ньютона являются: 1) интервал времени (Dt = t2 – t1), 2) длина отрезка (  ), 3) масса (m), а также производных от них: 4) ускорение (
), 3) масса (m), а также производных от них: 4) ускорение (  ) и сила (
) и сила ( 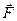 ).
).
Итак, уравнения Ньютона для материальной точки, а также для произвольных систем материальных точек одинаковы во всех инерциальных системах отсчета – инвариантны по отношению к преобразованию Галилея. Этот результат называется «механическим принципом относительности» (принципом относительности Галилея) и часто формулируется следующим образом: равномерное и прямолинейное замкнутой системы движение (относительно какой-либо инерциальной системы отсчета) не влияет на закономерности протекания в ней механических процессов. Следовательно, в механике все инерциальные системы отсчета совершенно равноправны. Другими словами, нельзя выделить из множества инерциальных систем отсчета какую-то «главную» инерциальную систему отсчета, которая обладала бы какими-либо преимуществами перед другими (так что движение тел относительно нее можно было бы рассматривать как «абсолютное движение», а покой – как «абсолютный покой»).
Дата добавления: 2015-02-09; просмотров: 370; Мы поможем в написании вашей работы!; Нарушение авторских прав |