
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Динамика вращательного движения твердого тела
Рассмотрим произвольную механическую систему, состоящую из n материальных точек. Пусть  - сила, действующая на i-ую материальную точку со стороны k-ой материальной точки, а
- сила, действующая на i-ую материальную точку со стороны k-ой материальной точки, а  - равнодействующая внешних сил, действующих на i-ую материальную точку системы. По второму закону Ньютона (см. (2.1.14)) уравнение движения материальной точки может быть представлено в виде:
- равнодействующая внешних сил, действующих на i-ую материальную точку системы. По второму закону Ньютона (см. (2.1.14)) уравнение движения материальной точки может быть представлено в виде:  Причем
Причем  так как i-ая материальная точка на себя не действует. Умножим векторно
так как i-ая материальная точка на себя не действует. Умножим векторно 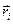 - радиус-вектор, проведенный в i-ую материальную точку из начала координат, на уравнение движения материальной точки. Получим
- радиус-вектор, проведенный в i-ую материальную точку из начала координат, на уравнение движения материальной точки. Получим

| (2.2.1,а) |
Легко видеть, что из левой части выражения (2.2.1,а) можно вынести дифференциал  . Действительно, так как
. Действительно, так как  (из определения векторного произведения), то
(из определения векторного произведения), то  . Таким образом,
. Таким образом,
 . .
| (2.2.1,б) |
Векторное произведение  на
на  называют
называют 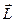 - моментом импульса материальной точки (в СИ единица измерения момента импульса -
- моментом импульса материальной точки (в СИ единица измерения момента импульса -  ):
):
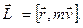 , ,
| (2.2.2) |
где  - радиус-вектор, проведенный из точки О в точку А (рис. 2.3);
- радиус-вектор, проведенный из точки О в точку А (рис. 2.3);  - импульс материальной точки;
- импульс материальной точки; 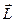 - псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
- псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от  к
к  .
.
 |
Векторное произведение радиуса - вектора
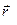 , проведенного из точки О в точку А приложения силы
, проведенного из точки О в точку А приложения силы  , на эту силу, называется моментом
, на эту силу, называется моментом  силы
силы 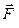 относительно точки O (момент силы в системе СИ измеряют в
относительно точки O (момент силы в системе СИ измеряют в  ):
):

| (2.2.3,а) |
 |
Векторы 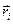 ,
,  и
и  образуют правую тройку векторов (рис. 2.4.).
образуют правую тройку векторов (рис. 2.4.).
Численное значение момента силы можно определить как:
| M = F×r×sina = F×l, | (2.2.3,б) |
где a - угол между векторами  и
и 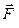 , l=r×sina – плечо силы, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы В (рис. 2.4). Из уравнений (2.2.1,б), (2.2.2) и (2.2.3,а) следует, что:
, l=r×sina – плечо силы, т.е. длина перпендикуляра, опущенного из точки О на линию действия силы В (рис. 2.4). Из уравнений (2.2.1,б), (2.2.2) и (2.2.3,а) следует, что:

| (2.2.4,а) |
Или для системы, состоящей из n точек:

 …………………………………………..
…………………………………………..

| (2.2.4,б) |
Сложим почленно полученные выше уравнения:

| (2.2.5) |
Отметим, что суммарный вектор

| (2.2.6) |
называют главным моментом внешних сил относительно точки О, а вектор

| (2.2.7,а) |
моментом импульса системы материальных точек.
Используя формулу связи линейной и угловой скорости  , получим
, получим
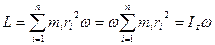 , ,
| (2.2.8) |
т.е. момент импульса твердого тела относительно оси Z равен произведению момента инерции Iz относительно той же оси на угловую скорость.
Продифференцировав уравнение (2.2.8) по времени получим:
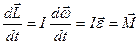 или
или

| (2.2.9) |
В соответствие с (2.2.9), скорость изменения момента импульса системы относительно неподвижной точки равна результирующему моменту (относительно той же точки) всех внешних сил, действующих на систему – основной закон динамики вращательного движения для системы материальных точек.
Рассмотрим случай, когда твердое тело закреплено в двух неподвижных точках O и O1. В этом случае вращение тела можно рассматривать вокруг некоторой оси, например OZ. Такое вращение происходит под действием составляющей момента внешних сил  . Из уравнения (2.2.9) следует, что:
. Из уравнения (2.2.9) следует, что:

| (2.2.10) |
Здесь 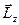 ,
,  - составляющие векторов момента импульса тела и результирующего момента внешних сил относительно точки О, направленные вдоль неподвижной оси OZ вращения тела и называемые, соответственно, моментом импульса тела относительно оси OZ и главным моментом внешних сил относительно той же оси. Уравнение (2.2.10) является основным законом динамики для тела, вращающегося вокруг неподвижной оси.
- составляющие векторов момента импульса тела и результирующего момента внешних сил относительно точки О, направленные вдоль неподвижной оси OZ вращения тела и называемые, соответственно, моментом импульса тела относительно оси OZ и главным моментом внешних сил относительно той же оси. Уравнение (2.2.10) является основным законом динамики для тела, вращающегося вокруг неподвижной оси.
Сумму произведений масс материальных точек тела на квадрат расстояния от точек до оси вращения называют моментом инерции тела относительно этой оси  (единицы измерения
(единицы измерения  в СИ -
в СИ -  ):
):

| (2.2.11) |
На практике при вычислении момента инерции тела его мысленно разбивают на бесконечно большое число малых элементов с массами dm и выражение (2.2.11) принимает вид:
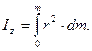
Вычислим в качестве примера момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр (рис.2.5).
 |
Поскольку диск однороден, плотность можно вынести из-под знака интеграла. Элемент объема диска dV = 2πr·b·dr, где b— толщина диска. Таким образом,
 ,
,
где R — радиус диска. Введя массу диска, равную произведению плотности на объем диска π·R2 b, получим:
 .
.
Нахождение момента инерции диска в рассмотренном примере облегчалось тем, что тело было однородным и симметричным, а момент инерции вычислялся относительно оси симметрии тела. В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы о переносе осей инерции (теорема Штейнера): момент инерции тела I относительно произвольной оси ОО1 равен сумме момента инерции тела IC относительно оси O/O/1, проведенной через центр инерции тела параллельно оси ОО1 и произведения массы m тела на квадрат расстояния между этими осями (рис. 2.6):
| I = IC + m×d2. | (2.2.12) |
 |
Например, момент инерции диска относительно оси О' в соответствии с теоремой Штейнера:

В таблице 2 представлены формулы вычисления моментов инерции однородных тел простейших геометрических форм.
Таблица 2.
| № | Тело | Положение оси OZ | Момент инерции I |
| Полый тонкостенный цилиндр (обруча) радиусом R и массой m. | Ось симметрии | 
| |
| Сплошной цилиндр (диск) радиусом R и массой m. | Ось симметрии | 
| |
| Прямой тонкий стержень длиной l и массой m. | Ось перпендикулярная стержню и проходит через его середину | 
| |
| Прямой тонкий стержень длиной l и массой m. | Ось перпендикулярная стержню и проходит через его конец | 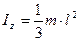
| |
| Шар радиусом R и массой m. | Ось проходит через центр шара | 
| |
| Шар радиусом R и массой m. | Ось проходит на расстоянии d от центра шара | 
|
Основное уравнение динамики вращательного движения тела относительно неподвижной оси (2.2.10) можно записать в виде:

| (2.2.13) |
Если тело абсолютно твердое, то его момент инерции Iz не зависит от времени и, как следствие,  , или
, или

| (2.2.14) |
Из выражения (2.2.14) видно, что угловое ускорение твердого тела, вращающегося относительно неподвижной оси OZ, прямо пропорционально результирующему моменту (относительно этой оси) действующих на тело всех внешних сил, и обратно пропорционально моменту инерции тела относительно той же оси (второй закон Ньютона во вращательном движении). Таким образом, момент инерции является мерой инертности тела во вращательном движении.
Закон сохранения момента импульса
Если внешние силы отсутствуют (система замкнута) или таковы, что их суммарный момент равен нулю ( 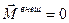 ), то выражение (2.2.10) примет вид:
), то выражение (2.2.10) примет вид:
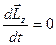 и и  или
или

| (2.2.15) |
Уравнение (2.2.15) называют законом сохранения момента количества движения.
В целом, сравнительный анализ характеристик поступательного и вращательного движения представлен в таблице 3.
Таблица 3.
| Характеристики движения | Поступательное движение (материальная точка) | Вращательное движение (твердое тело, закрепленное на оси |
| Кинематические характеристики | ||
| Изменение положения | Вектор перемещения (путь)

| Угол поворота

|
| Быстрота движения | Линейная скорость

| Угловая скорость

|
| Ускорение | Линейное ускорение

| Угловое ускорение

|
| Динамические характеристики и законы движения | ||
| Мера инертности | Масса тела m | Момент инерции I |
| Фундаментальные характеристики движения | Импульс тела

| Момент импульса твердого тела относительно оси ОZ
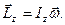
|
| Внешнее воздействие | Сила
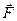
| Момент силы относительно оси ОZ Mz |
| Второй закон Ньютона | 
| 
|
| Основное уравнение динамики | 
| 
|
| Законы сохранения | Закон сохранения импульса
 если
если 
| Закон сохранения момента импульса
 или или  ,
если ,
если 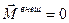
|
| Кинетическая энергия | 
| 
|
Дата добавления: 2015-02-09; просмотров: 291; Мы поможем в написании вашей работы!; Нарушение авторских прав |