Кинематика материальной точки и поступательного движения твердого тела

Система отсчета. Траектория.

Длина пути и вектор перемещения

Для описания движения тела в пространстве и времени используют физические модели:

· Материальной точкой (тело точечной массы) называется идеализированная модель, соответствующая физическому телу, размерами которого в данных условиях можно пренебречь.

· Абсолютно твердое тело – тело, расстояние между двумя точками которого в условиях данной задачи можно считать постоянным. Иначе говоря - это тело, формы и размеры которого не изменяются при его движении.

· Абсолютно упругое тело – тело, деформация которого подчиняется закону Гука, а после прекращения внешнего силового воздействия восстанавливает свои первоначальные размеры и форму

· Абсолютно неупругое тело – тело, сохраняющее деформированное состояние после прекращения действия внешних сил.

Всякое тело можно мысленно разбить на большое число частей, сколь угодно малых по сравнению с размерами всего тела. Каждую такую часть можно рассматривать как материальную точку, а само тело или любую систему тел – как систему материальных точек.

Положение тел в пространстве можно определить только по отношению к другим телам. Абсолютно твердое тело, по отношению к которому рассматривают движение исследуемого тела, называется системой отсчета. С системой отсчета жестко связывают систему координат, так что положение любой точки определятся значениями трех координат этой точки. Наиболее часто пользуются прямоугольными декартовыми координатами: x, y, z (рис.1.1.).

Положение точки М относительно системы отсчета можно задать не только с помощью трех ее декартовых координат x, y, z, но также с помощью векторной величины - проведенного в точку М из начала системы координат (точки О) радиуса - вектора 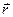(рис. 1.1). Если 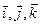- единичные вектора осей прямоугольной декартовой системы координат, то

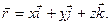
(1.1.1)

При движении материальной точки М ее координаты x, y, z и 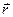меняются со временем. Поэтому для определения положения материальной точки в любой момент времени (t) вводятся уравнения, которые в декартовой системе координат имеют вид:

,

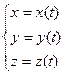(1.1.2,а)

или в более общей записи

.

(1.1.2,б)

Зависимости (1.1.2,а) и (1.1.2,б) называются кинематическими уравнениями движения материальной точки.

Совокупность всех последовательных положений материальной точки в пространстве представляет траекторию движения. В зависимости от формы траектории различают прямолинейное и криволинейное движение точки. Движение точки называется плоским, если ее траектория целиком лежит в одной плоскости.

Вектором перемещения материальной точки за время 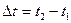называется вектор, проведенный из положения этой точки в момент времени t₁ в ее положение в момент t₂ (рис. 1.2.). Он равен приращению радиус-вектора 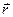за рассматриваемый промежуток времени Dt:

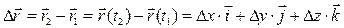
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории.

Для измерения длины пути и перемещения используют меру длины – метр (м) в системе СИ и – сантиметр (см) в системе СГС.

Материальная точка, свободно движущаяся в пространстве, может совершать только три независимых движения. Например, движение точки вдоль каждой из осей прямоугольной декартовой системы координат нельзя осуществить за счет ее движения вдоль остальных двух осей. Число независимых движений, которые может совершать механическая система, называется числом степеней свободы этой системы. Следовательно, свободная материальная точка имеет три степени свободы.