
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Рівняння руху.
| Рівномірний рух | ||||||
| Рівномірний рух (вздовж лінії траєкторії) | Рівномірний рух по колу (вздовж окружності) |  Рівномірний рух по колу(кутові характеристики) Рівномірний рух по колу(кутові характеристики)
| ||||
  - довжина пройденого
шляху. - довжина пройденого
шляху.
 – швидкість тіла. – швидкість тіла.
|   - довжина пройденого шляху
(довжина дуги), яку пройшло тіло
R вздовж окружності. - довжина пройденого шляху
(довжина дуги), яку пройшло тіло
R вздовж окружності.
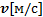 – швидкість тіла вздовж
лінії окружності. – швидкість тіла вздовж
лінії окружності.
|  𝛗 𝛗  - кут, на який повернувся
𝛗 радіус-вектор, є мірою пройденого
шляху. - кут, на який повернувся
𝛗 радіус-вектор, є мірою пройденого
шляху.
 - кутова швидкість тіла - кут,
на який повертається радіус-вектор за 1 сек. - кутова швидкість тіла - кут,
на який повертається радіус-вектор за 1 сек.
| ||||

| 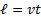
 (Довжина всієї окружності) (Довжина всієї окружності)
| 
| ||||

| 
| 
| ||||
| Рівноприскорений рух | ||||||
| Рівно-прискорений рух вздовж траекторії | Рух тіла під дією сили тяжіння |  Рівноприскорений рух по колу Рівноприскорений рух по колу
|  Рівноприскорений рух по колу (кутові характеристики) Рівноприскорений рух по колу (кутові характеристики)
| |||
  - прискорення - прискорення
величина, на яку збільшується швидкість тіла за 1 секунду |    прискорення вільного
h падіння у грав. полі.
прискорення вільного
h падіння у грав. полі.
|   - прискорення
тіла вздовж лінії окружності
R (тангенціальне) - прискорення
тіла вздовж лінії окружності
R (тангенціальне)
|  ε ε  -кутове
𝛗 прискорення
R -кутове
𝛗 прискорення
R
| |||
 - довжина пройденого шляху - довжина пройденого шляху
|  - висота - висота
|  - довжина пройденого шляху (довжина дуги), яку пройшло тіло вздовж окружності. - довжина пройденого шляху (довжина дуги), яку пройшло тіло вздовж окружності.
| 𝛗  - кут, на який повернувся радіус-вектор, є мірою пройденого шляху. - кут, на який повернувся радіус-вектор, є мірою пройденого шляху.
| |||
 - миттєве значення швидкості тіла - миттєве значення швидкості тіла
|  - миттєве значення швидкості тіла - миттєве значення швидкості тіла
|  - миттєве значення швидкості тіла вздовж лінії окружності - миттєве значення швидкості тіла вздовж лінії окружності
|  - миттєве значення кутової швидкості тіла - миттєве значення кутової швидкості тіла
| |||

| 
| 
| 
| |||

| 
| 
| 
| |||

| 
| 
| 
| |||

| 
| 
| 
| |||
| Зв'язок лінійних та кутових характеристик | ||||||
Увага! Ці формули справедливі, якщо кутові характеристики мають розмірність радіан!
𝛗  , ,  ε ε 
|  ( пройдений шлях → кут) ( пройдений шлях → кут)
 (швидкість → кутова швидкість) (швидкість → кутова швидкість)
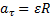 (прискорення вздовж лінії окружності (тангенціальне) → кутове прискорення) (прискорення вздовж лінії окружності (тангенціальне) → кутове прискорення)
| |||||
Доцентрове прискорення (або нормальне 
нормальне краще розглядати окремо. Для цього прискорення існують такі дві формули:
(У системі відліку, пов’язаній з тілом, з’являється так зване центробіжне прискорення, яке дорівнює доцентровому, але протилежне йому за напрямком).
| |||
Існує зв'язок між доцентровим прискоренням  та прискоренням вільного падіння та прискоренням вільного падіння  .
Якщо тіло просто падає вниз, то прискорення вільного падіння ( .
Якщо тіло просто падає вниз, то прискорення вільного падіння (  Якщо надати тілу горизонтальну складову швидкості
Якщо надати тілу горизонтальну складову швидкості  , то воно буде рухатися , то воно буде рухатися      по параболі з певною кривизною. Але, якщо швидкість буде достатньо великою, такою, щоб кривизна траєкторії була як у планети Земля, то тіло стане її супутником. (Супутник рухається вздовж окружності, як правило, з постійною швидкістю по параболі з певною кривизною. Але, якщо швидкість буде достатньо великою, такою, щоб кривизна траєкторії була як у планети Земля, то тіло стане її супутником. (Супутник рухається вздовж окружності, як правило, з постійною швидкістю  .) .)
|
Дата добавления: 2015-02-09; просмотров: 404; Мы поможем в написании вашей работы!; Нарушение авторских прав |

 ). Воно не впливає ні на швидкість руху тіла вздовж лінії окружності, ані на кутову швидкість. Тому його
). Воно не впливає ні на швидкість руху тіла вздовж лінії окружності, ані на кутову швидкість. Тому його 

