
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неустановившееся истечение жидкости из резервуаров.
Истечение из резервуара произвольной формы с постоянным притоком. Резервуары являются наиболее распространёнными хранилищами различных жидкостей. К наиболее существенным технологическим операциям с резервуарами относятся операции заполнения резервуаров и операции опорожнения. Если операция заполнения никаких существенных проблем перед гидравликой не ставит, то опорожнение резервуара может рассматриваться как прямая гидравлическая задача.
Пусть, в самом общем случае, имеем резервуар произвольной формы (площадь горизонтального сечения резервуара является некоторой функцией его высоты). В резервуар поступает жидкость с постоянным расходом Q0. Задача сводится к нахождению времени
необходимого для того, чтобы уровень жидкости в резервуаре изменился с высоты взлива 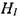 до
до  . Отметим, что площадь горизонтального сечения резервуара несоизмеримо велика по сравнению с площадью живого сечения вытекающей струи жидкости, т. е величиной скоростного напора в резервуаре можно пренебречь (уровень жидкости в резервуаре меняется с весьма малой скоростью).
. Отметим, что площадь горизонтального сечения резервуара несоизмеримо велика по сравнению с площадью живого сечения вытекающей струи жидкости, т. е величиной скоростного напора в резервуаре можно пренебречь (уровень жидкости в резервуаре меняется с весьма малой скоростью).
Величина расхода при истечении жидкости является переменной и зависит от напора, т.е. текущей высоты взлива жидкости в резервуаре  Уровень жидкости в резервуаре будет подниматься, если
Уровень жидкости в резервуаре будет подниматься, если  и снижаться когда
и снижаться когда 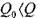 , при притоке
, при притоке
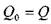 уровень жидкости в резервуаре будет постоянным. Поскольку движение жидкости при истечении
уровень жидкости в резервуаре будет постоянным. Поскольку движение жидкости при истечении  из отверстия является неустановившемся, решение поставленной задачи осуществляется методом смены стационарных состояний. Зафиксируем уровень жидкости в резервуаре на отметке
из отверстия является неустановившемся, решение поставленной задачи осуществляется методом смены стационарных состояний. Зафиксируем уровень жидкости в резервуаре на отметке 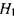 . Этому уровню будет соответствовать расход жидкости при истечении из отверстия:
. Этому уровню будет соответствовать расход жидкости при истечении из отверстия:
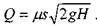
За бесконечно малый интервал времени из резервуара вытечет объём жидкости равный:

За этот же интервал времени в резервуар поступит объём жидкости равный:

Тогда объём жидкости в резервуаре изменится на величину  :
:

Выразив величину притока жидкости в резервуар Qo подобно расходу Q, получим:

Тогда время, за которое уровень жидкости изменится на величину dH :

Для дальнейшего решения резервуар следует разбить на бесконечно тонкие слои, для которых можно считать, что площадь сечения резервуара в пределах слоя постоянна.
Тем не менее, практического значения задача (в общем виде) не имеет. Чаще всего требуется искать время полного опорожнения резервуара правильной геометрической формы: вертикальный цилиндрический резервуар (призматический), горизонтальный цилиндрический, сферический.
Истечение жидкости из вертикального цилиндрического резервуара. Вертикальный цилиндрический резервуар площадью поперечного сечения S заполнен жидкостью до уровня Н. Приток жидкости в резервуар отсутствует. Тогда дифференциальное уравнение истечения жидкости будет  иметь вид:
иметь вид:
i 
Для начала определим время необходимое для перемещения уровня жидкости с отметки  до
до 

Когда  = Н а
= Н а  = 0, то время полного опорожнения резервуара составит:
= 0, то время полного опорожнения резервуара составит:

Таким образом, время полного опорожнения резервуара в два раза больше, чем время истечения этого же объёма жидкости при постоянном напоре равном максимальному напору Я.
Истечение жидкости из горизонтального цилиндрического резервуара. В отличие от вертикального резервуара, площадь сечения свободной поверхности и горизонтального сечения резервуара - величина переменная и зависит от уровня жидкости в резервуаре.

Время полного опорожнения резервуара:

или, обозначив: D = 2  получим:
получим:

Переток жидкости между резервуарами при переменных уровнях жидкости. Если два резервуара соединены между собой, то при разных уровнях жидкости в этих резервуарах будет происходить переток жидкости из резервуара с более высоким положением уровня свободной поверхности в резервуар, где эта поверхность будет расположена на более низкой отметке. Переток будет осуществляться при переменном (убывающем) расходе и продолжаться до тех пор, пока уровни жидкости в обоих резервуарах не сравняются.
Рассмотрим два резервуара А и В, соединённые между собой трубопроводом с площадью сечения s. Питающий резервуар А имеет более высокий уровень жидкости
С - С' относительно плоскости сравнения О - О, который равен  , площадь сечения резервуара А равна
, площадь сечения резервуара А равна  . Приёмный резервуар В имеет более низкий уровень жидкости D - D', который относительно плоскости сравнения равен z2,
. Приёмный резервуар В имеет более низкий уровень жидкости D - D', который относительно плоскости сравнения равен z2,  площадь сечения этого резервуара -
площадь сечения этого резервуара -  . Переток жидкости
. Переток жидкости
обеспечивается переменным действующим напором равным Н =  . Поскольку оба
. Поскольку оба
этих уровня меняются во времени,, то и действующий напор Я тоже будет переменным.
Пусть начальный действующий напор будет равен 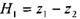 , а действующий на-
, а действующий на-
пор на конец интересующего нас периода будет равным  (в общем случае он может быть не равен 0). Тогда за время dt из резервуара А в резервуар В при некотором напоре Я через соединительный трубопровод перетечёт объём жидкости равный:
(в общем случае он может быть не равен 0). Тогда за время dt из резервуара А в резервуар В при некотором напоре Я через соединительный трубопровод перетечёт объём жидкости равный:
 ?
?
где: 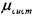 - коэффициент расхода системы, т.е. соединительного трубопровода.
- коэффициент расхода системы, т.е. соединительного трубопровода.
При этом в резервуаре А уровень жидкости понизится на величину 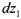 , а в резервуаре В, наоборот, повысится на величину . При этом действующий напор также изменится на величину:
, а в резервуаре В, наоборот, повысится на величину . При этом действующий напор также изменится на величину:

Изменения уровней жидкости в резервуарах будут связаны между собой:
 ?
?
Тогда:
 •>
•>
откуда:

Поскольку площадь сечения резервуара постоянная, то необходимо лишь выразить  через действующий напор Н.
через действующий напор Н.
 , тогда:
, тогда:  , откуда:
, откуда:

Окончательно:
 > или:
> или:

В том случае, когда уровни в резервуарах сравняются  :
:
Дата добавления: 2015-02-09; просмотров: 254; Мы поможем в написании вашей работы!; Нарушение авторских прав |