
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Неустановившееся движение жидкости в трубопроводе 9.1. Постановка вопроса, требования к модели и допущения
Вопросы изучения неустановившегося движения реальной жидкости очень сложны. Если окажется необходимым получить самое общее решение поставленной задачи, то придётся рассматривать систему уравнений, в составе которой будут входить:
уравнение Навье-Стокса,
уравнение неразрывности,
уравнение состояния жидкости,
- уравнение термического состояния жидкости, уравнение первого закона термодинамики.
Следует отметить, что данная система настолько сложна и трудоёмка в своём решении, что сразу же стоит рассмотреть вопросы о необходимости принятия некоторых допущений и ограничений, облегчающих решение поставленной задачи. Другими словами, необходимо определить из соображений практики степень детальности построения модели, откуда станут очевидными требования к описанию объекта изучения. Так, рассматриваемый объект (жидкость) должна обладать упругими свойствами (быть сжимаемой), деформация жидкости должна происходить в пределах пропорциональности, что соответствует закону Гука. Следует также учитывать упругие свойства самого трубопровода, другие внешние среды не рассматриваются. Движение жидкости считается одномерным. Можно также пренебречь и теплопотерями во внешнюю среду.
Приняв такие ограничения, можно полную систему уравнений заменить на систему из двух дифференциальных уравнений  Н.Е. Жуковского:
Н.Е. Жуковского:
где: 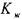 - адиабатический модуль упругости жидкости.
- адиабатический модуль упругости жидкости.
Однако даже для решения этой довольно простой системы придётся преодолеть немалые трудности. По сути дела обычно рассматривают одну из хорошо известных моделей процесса неустановившегося движения жидкости: модель несжимаемой жидкости,
- модель сжимаемой жидкости с сосредоточенными параметрами,
- модель сжимаемой жидкости с рассосредоточенными параметрами.
Строго говоря, процесс изменения давления в жидкости во времени уподобляется волновым процессам в упругой среде, модель среды должна относиться к моделям с рас-
пределёнными параметрами. Однако подходить к выбору модели следует, прежде всего, исходя из практики работы предприятий горных отраслей промышленности. По этой причине остановимся на изучении проблем, связанных с явлением гидравлического удара в круглых трубах и на базе решения этой практической задачи рассмотрим основные уравнения неустановившегося движения жидкости. Явление гидравлического удара характеризуется большими скоростями распространения ударной волны и значительными величинами возникающих при этом давлений, периоды колебаний давления составляют доли секунды, благодаря чему действием сил трения можно пренебречь. 9.2. Явление гидравлического удара
Явление гидравлического удара возникает при резком изменении скорости движения жидкости в трубопроводе (вплоть до его мгновенного закрытия). В таких случаях происходит переход кинетической энергии движущейся жидкости в потенциальную энергию покоящейся жидкости. Однако такой переход не мгновенный, а протекает с определённой скоростью, зависящей от свойств жидкости и материала трубопровода. Кроме того, этот процесс носит волновой характер. Покажем на простом примере, что гидравлический удар - процесс колебательный, т.е. волновой.
Резервуар А соединён с трубопроводом длиной /, на конце трубопровода установлена задвижка. Размеры резервуара таковы, что при отборе жидкости из него уровень жидкости в резервуаре практически не понижается. Также для упрощения модели пока будем считать саму трубу недеформируемой. Примем за начало отсчёта точку О, расположенную на оси трубы в плоскости задвижки. Если потерями напора на трение при движении жидкости пренебречь, то пьезометрическая линия будет горизон 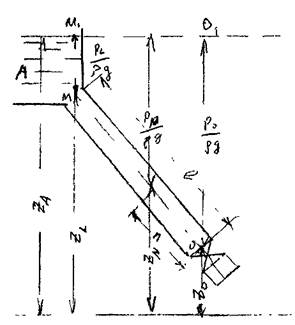 тальной. Если бы жидкость была несжимаемой, то при резком закрытии задвижки
тальной. Если бы жидкость была несжимаемой, то при резком закрытии задвижки
мгновенно остановилась бы вся масса жидкости находящаяся в трубе, что вызвало бы мгновенный рост давления во всей жидкости. На самом деле в упругой жидкости процесс будет развиваться иначе. В момент резкого закрытия задвижки остановится только тонкий слой жидкости, непосредственно примыкающий к задвижке, остальная масса жидкости
будет продолжать движение За бесконечно малый промежуток времени (длительность процесса остановки) остановится масса жидкости в объеме первого тонкого слоя.

где: -  - толщина тонкого слоя жидкости,
- толщина тонкого слоя жидкости,
S - площадь внутреннего сечения трубы.
Если обозначить давление в точке О до закрытия затвора через 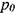 , а через
, а через  дав-
дав-
ление после мгновенного закрытия задвижки, то по теореме об изменении количества движения можно вычислить 
или:  где:
где: 
Или; 
Затем в следующий момент времени остановится следующий слой жидкости, потом третий и т.д. Так постепенно увеличенное давление у задвижки распространится по всему
трубопроводу в направлении против течения жидкости Тогда величина  представ-
представ-
ляет собой скорость распространения упругой (ударной) волны. По истечении времени 
вся жидкость в трубопроводе станет находиться в сжатом состоянии. Но теперь возник перепад давления между жидкостью в резервуаре и жидкостью в трубе, в результате чего начнётся движение упругой жидкости из трубопровода обратно в резервуар. По истечении
такого же временного интервала  , давление жидкости у задвижки понизится на величину
, давление жидкости у задвижки понизится на величину  , т.е достигнет первоначального значения. При этом процесс движения жидкости в резервуар будет продолжаться, пока пониженное давление не распространится до конца трубопровода (до резервуара). Таким образом, давление у задвижки буде сохраняться на
, т.е достигнет первоначального значения. При этом процесс движения жидкости в резервуар будет продолжаться, пока пониженное давление не распространится до конца трубопровода (до резервуара). Таким образом, давление у задвижки буде сохраняться на
постоянном уровне в течение времени  , а продолжительность всего цикла гидравлического удара будет равна
, а продолжительность всего цикла гидравлического удара будет равна  . За это время давление у задвижки в течение половины этого
. За это время давление у задвижки в течение половины этого
времени будет максимальным  , в течение другой половины времени - минималь-
, в течение другой половины времени - минималь-
ным 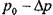
Дата добавления: 2015-02-09; просмотров: 266; Мы поможем в написании вашей работы!; Нарушение авторских прав |