Классификация. Теоретические основы классификaции

Теоретические основы классификaции

Классификация происходит в условиях свободного или стесненного падения зерен. Свободное падение представляет собой движение единичных зерен в среде, исключающей их взаимное воздействие друг на друга. Под стесненным падени­ем понимается движение множества зерен в виде такой массы, когда помимо гравитационных сил и сил сопротивления сре­ды на движение зерен оказывает влияние динамическое воз­действие непрерывно сталкивающихся окружающих зерен.

Скорость свободного падения зерна определяется соотношением силы тяжести, подъемной (архимедовой) силы и силы сопротивления среды, которая зависит от режима движения зерна.

При ламинарном режиме тело движется с малой скоростью, потоки среды как бы омывают его, не образуя завихрений. Сопротивление Р_в определяется главным образом вязкостью среды μ и количественно описывается законом Стокса:

Рв = 3 πμνd (1)

где ν — скорость движения зерна; d -диаметр зерна.

Турбулентный режим движения характерен для высоких скоростей движения и сопровождается образованием вихрей у поверхности тела и позади него. Динамическое или инерционное сопротивление среды перемещению тела изменяется в этом случае по закону Ньютона — Риттингера:

(2)

где k— коэффициент (равный 1/2, по Риттингеру); F— площадь проекции тела (равна πd²/4 для шара); ∆—плотность среды.

В реальных условиях движущееся зерно испытывает одновременное действие как сопротивления от вязкости Рв, так и динамического сопротивления Рд, но степень их проявления различна. Характеристикой соотношения сил сопротивлений Рд и Рв и, следовательно, режима движения минерального зерна в среде является безразмерный параметр Рейнольдса (Rе)

откуда в общем виде:

(3)

При значениях Rе < 1 наблюдается ламинарный режим движения частиц, размер которых не превышает 0,1 мм. При значениях Rе > 1000 и размере частиц более 2 мм наблюдается турбулентный режим движения. Переходной области от ламинарного к турбулентному режиму движения отвечают значения Rе от 1 до 1000, а крупность частиц от 0,1 до 2 мм. Сопротивление среды для этой области можно рассчитать по формуле Аллена:

(4)

Если подставить значение μ из формулы (3) в выражение (1)

(5)

и сравнить выражения для Р_д [формула (2)], для Р_а [формула (4)] и для Р_в [формула (5)], то обнаружим, что общий закон сопротивления среды движению зерна описывается формулой

(6)

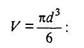
где φ =f(Re) - коэффициент сопротивления. Графическое изображение зависимости φ = f(Re) в логарифмических координатах, носящее название диаграммы Рейлея (рис. 1, кривая φ ), указывает на постепенный переход от ламинарного к турбулентному режиму движения по мере возрастания параметра Rе. Гравитационная сила G, вызывающая падение зерна, будет определяться весом тела в среде. В соответствии с законом Архимеда для шарообразного тела объемом: V=πd³/6

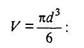
Рисунок 5-Зависимость коэффициента сопротивления ψ и праметра Rе² ψ от числа Рейнольдса (Rе)

(8)

где δ — плотность зерна; g— ускорение силы тяжести.

Результирующая сила Р₁, ускоряющая движение зерна в среде, определится как разность между гравитационной силой Gи силой сопротивления Р [формула (7)]:

Увеличение скорости движения частиц в начальный момент под действием гравитационной силы вызывает возрастающее сопротивление среды и через доли секунды частица начинает падать с постоянной скоростью ν₀.

откуда (для общего случая):

(9)

При ламинарном режиме, на основании уравнений (1) и (8):

(10)

При переходном режиме, на основании формул (4) и (8):

С учетом выражения для Rе:

(11)

При турбулентном режиме, на основании формул:

(12)

Универсальный метод, пригодный для определения конечных скоростей движения зерен любой крупности, плотности, формы, предложил П.В. Лященко. Он учел, что на основании формул (3) и (6) можно составить систему уравнений:

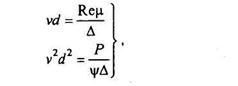(13)

в результате совместного решения которой получим выражение для параметра Rе²ψ

(14)

Поскольку при установившемся движении Р=Ġ, то, подставляя в формулу (3.18) вместо Р выражение для Ġ из формулы (3.11), находим:

(15)

По уравнению (15) на основании известных параметров зерна и среды легко рассчитать значение параметра Rе²ψ и использовать его для для определения параметра Рейнольдса по диаграмме Rе² ψ =f (Rе), построенной на основе диаграммы Рейлея ψ =f (Rе), и изображенной на рисунке 1. После этого можно определить конечную скорость падения частицы или непосредственной подстановкой полученного значения Rе в формулу 3 или подстановкой значения ψ найденного по значению Rе на диаграмме Рейлея (см. рис. 1, кривая ψ), в формулу (9).