Сложное движение точки. Если материальная точка участвует сразу в двух движениях, то такое движение называется сложным

Если материальная точка участвует сразу в двух движениях, то такое движение называется сложным. Движение точки относительно подвижной системы отсчета называется относительным, и его кинематические характеристики имеют верхний индекс «r». Движение же точки вместе с подвижной системой отсчета называется – переносным (имеет индекс «е»). Суммарное или результирующее движение точки относительно неподвижной системы отсчета (часто она связана с землей) называется – абсолютным (индекс «а»).

В этом случае для кинематических характеристик справедливы следующие зависимости

, (5)

где – кориолисово ускорение, возникающее из-за взаимодействия переносного и относительного движений.

Оно определяется по правилам векторного произведения, т.к. . Вектор результат перпендикулярен плоскости, в которой лежат вектора сомножители и направлен по правилу правого винта, если первый вектор кратчайшим путем совмещать со вторым . При этом вектор – угловой скорости переносного движения всегда лежит на оси переносного вращения (в любой точке) и направлен согласно правилу правого винта, примененному к известному направлению вращ ения (рис. 3).

Рис. 3

По модулю 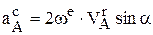, и оно может быть равно нулю в двух случаях: если параллельно , т.е. a=0, и если переносное движение не связано с поворотом подвижной системы отсчета (её оси перемещаются параллельно самим себе, т.е. поступательно и ).

Если переносное или относительное движение точки являются криволинейными, то в выражениях (5) удобно соответствующее ускорение разложить на два вектора: касательного и нормального ускорения, например .

Уравнения (5) могут быть решены двумя очень распространенными в кинематике способами: графическим или аналитическим, при условии, если в них содержится только две неизвестные. При этом под неизвестными отдельно понимаются модуль (величина) или направление какого-то из векторов. Чаще всего при решении задач можно встретить два случая. Первый, когда из (5) необходимо найти величину и направление одного вектора или , а для остальных векторов величины и направления (углы с одной из осей Х или Y) заданы или легко находятся по исходным данным задачи. Второй случай, когда все вектора в одном из выражений (5) известны по направлению, а надо найти величины двух из них, например .

Графический способ предполагает рисование векторов, входящих в (5) с использованием заранее выбранного масштаба. Тогда при сложении векторов конец первого является началом второго вектора или через него проводят прямую, если известно только направление второго вектора. Результирующий вектор проводят из начала первого к концу последнего из складываемых векторов. В результате графического решения получается замкнутый многоугольник (треугольник), в котором искомые по величине вектора измеряют и умножают на выбранный масштаб для определения их величины (рис. 4).

Рассмотрим пример, в котором известные величины или направления векторов обозначим внизу штрихом, а неизвестные знаком вопроса

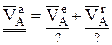направления

величины векторов

Однако наиболее часто применяется второй аналитический способ решения уравнений (5), когда их проецируют почленно на выбранные оси X и Y, а затем решают полученную систему двух алгебраических уравнений с двумя неизвестными. В рассмотренном выше примере, когда вектор задан по величине и направлению (ось X выбрана по направлению ), а вектора известны только по направлениям, заданными углами с осью X проецирование векторного уравнения на оси дает следующий результат:

для оси Х:

для оси Y:

Решение последней системы уравнений позволяет определить величины векторов ( должно быть известно или определено по исходным данным, например путем дифференцирования уравнений движения, как показано в (2) и (3)).

Рассмотрим две конкретные задачи с использованием уравнений (5) для сложного движения точки.