Задача 1. Здесь рычаг манипулятора поворачивается в горизонтальной плоскости и одновременно вдоль рычага перемещается ползун с захватом (материальная точка А) (рис

Здесь рычаг манипулятора поворачивается в горизонтальной плоскости и одновременно вдоль рычага перемещается ползун с захватом (материальная точка А) (рис. 5).

Рис. 5

Дано: 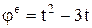(рад.), (м).

Найти: при t=1 c.

Решение: Движение точки А является сложным: относительное движение вдоль рычага и переносное, т.е. поворот вместе с рычагом.

Сначала определим положение точки А в её относительном движении при

t=1 c и найдем в этом положении 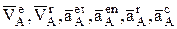по величине и направлению.

Для относительного движения

т.к. движение по прямой вдоль оси Х, то и 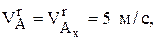аналогично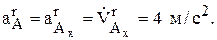

Для переносного движения:

– угловая скорость переносного движения;

– его угловое ускорение (знак « - » у w^e , полученный после дифференцирования и подстановки значения t означает, что направление вращения против положительного отсчета координаты j, принятого в задаче, а знак « + » у e^e означает, что направление ускорения совпадает с j);

– вращательная скорость перпендикулярна радиусу ОА и направлена в сторону w^e;

– перпендикулярна радиусу в сторону e^e;

– по радиусу к центру О.

.

Итак , т.к. перпендикулярно , то последнее уравнение можно не проецировать на оси Х и Y, а использовать теорему Пифагора

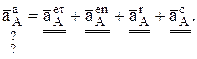
После проецирования на оси Х и Y получим