Теоретическое введение. Электрическое поле возникает вокруг тела, имеющего заряд

Электрическое поле возникает вокруг тела, имеющего заряд. Электрическое поле, созданное системой неподвижных зарядов, называется электростатическим полем. О величине электрического поля судят по силе, действующей на помещенный в это поле пробный заряд . Пробный заряд – это положительный, единичный, точечный заряд. Силовой характеристикой электрического поля является вектор напряженности :

. (1)

Напряженность – это векторная величина, характеризующая силу, с которой поле действует на положительный пробный заряд.

Если поле создается несколькими зарядами, то результирующее поле находится как векторная сумма напряженностей, созданных каждым зарядом в отдельности, т.е. по принципу суперпозиции:

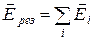. (2)

Напряженность поля, созданного точечным зарядом q, равна

. (3)

Силы, действующие на электрический заряд со стороны поля неподвижных зарядов, являются потенциальными. Это значит, что работа, совершаемая этими силами над перемещающимся точечным зарядом, не зависит от траектории движения этого заряда, а зависит лишь от его начального и конечного положений. Поле стационарных зарядов, в котором действуют такие силы, также называется потенциальным. Работа потенциальных сил при перемещении заряда совершается за счет уменьшения потенциальной энергии его взаимодействия с полем, т.е. .

Каждой точке потенциального поля можно сопоставить специальную скалярную функцию координат , называемую потенциалом. Потенциал численно равен потенциальной энергии единичного пробного заряда, помещенного в данную точку поля, т.е.

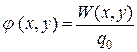, (4)

где – величина пробного заряда, – его потенциальная энергия в точке поля с координатами х и у (мы ограничиваемся двумя координатами, т.к. в нашей работе рассматривается поле в плоскости).

Если принять потенциал на бесконечности равным нулю, то потенциал можно представить как работу внешних сил по перемещению пробного заряда из бесконечности в данную точку поля. Тогда разность потенциалов – это работа внешних сил по перемещению пробного заряда из первой точки во вторую. В этом заключается физический смысл потенциала и разности потенциалов.

Между напряженностью и потенциалом существует зависимость, вытекающая из определения этих величин:

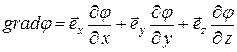, , (5)

где называется градиентом потенциала, и 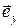единичные орты координатных осей. Таким образом, проекции вектора напряженности на координатные оси

. (6)

Для наглядного (графического) изображения поля используют силовые линии и эквипотенциальные поверхности.

Силовые линии – это геометрические линии, касательная к которым в каждой точке совпадает с направлением вектора напряженности . Это такая линия, по которой будет двигаться положительный точечный заряд, не имеющий начальной скорости. Напряженность поля в какой-либо точке поля пропорциональна плотности силовых линий, пересекающих площадку, перпендикулярную силовым линиям. Силовые линии электростатического поля начинаются на положительных зарядах и заканчиваются на отрицательных, или уходят в бесконечность.

Эквипотенциальные поверхности – поверхности равного потенциала – удовлетворяют условию . Эквипотенциальные поверхности и силовые линии взаимно перпендикулярны, а градиент потенциала направлен по нормали к эквипотенциальной поверхности и равен по модулю , где – расстояние по нормали между двумя эквипотенциальными поверхностями, потенциалы которых отличаются на бесконечно малую величину . Тогда

(7)

где – единичный вектор, направленный по нормали к эквипотенциальной поверхности. Таким образом, вектор направлен в сторону убывания потенциала.

Во всех практических приложениях вместо точной формулы (7) используют приближенную

. (8)