Теоретическое введение. Соленоид представляет собой катушку, по виткам которой течет ток

Соленоид представляет собой катушку, по виткам которой течет ток. Этот ток создает магнитное поле. О причинах возникновения магнитного поля и его свойствах прочитайте в работе 26. Наиболее простой вид картины силовых линий будет в случае бесконечно длинного соленоида. Опыт показывает, что чем длиннее соленоид, тем меньше индукция магнитного поля вне его. Для бесконечно длинного соленоида магнитное поле снаружи отсутствует вообще, а внутри его линии вектора направлены вдоль его оси, причем линии вектора составляют с направлением тока правовинтовую систему.

Магнитное поле в точках на оси соленоида конечной длины можно рассчитать, используя закон Био-Савара-Лапласа:

Индукция магнитного поля , созданного длинным проводом произвольной конфигурации, по которому течет ток I , равна векторной сумме индукций магнитных полей , созданных каждым элементом длины этого провода

, (1)

где – элемент тока, – радиус-вектор, проведенный от этого элемента до точки, в который определяем магнитное поле. Как видно из формулы, поле перпендикулярно плоскости, в которой лежат радиус-вектор и элемент тока. Модуль индукции, создаваемой элементом тока находится по формуле

, (2)

где – угол между радиус-вектором и элементом тока.

Использование этого закона дает формулу

, (3)

где I – ток в соленоиде, N – полное число витков в соленоиде, 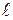– его длина, r- радиус соленоида, а – расстояние от края соленоида до той точки, в которой определяется значение магнитной индукции,

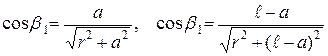. (4)

Если длина катушки в 5 раз превосходит ее диаметр, то магнитное поле на оси ее почти совпадает с полем бесконечно длинного соленоида. Для определения магнитного поля на оси бесконечно длинного соленоида удобнее воспользоваться теоремой о циркуляции вектора .

Циркуляция вектора индукции магнитного поля по любому замкнутому контуру равна алгебраической сумме всех токов, охватываемых этим контуром, умноженной на магнитную постоянную

,

где – элемент длины контура, по которому считают циркуляцию.

Следует помнить, что , где – угол между векторами и .

Если токи текут в разных направлениях, то положительным считают тот, направление которого связано с направлением обхода контура правилом правого винта.

Из симметрии магнитного поля соленоида следует, что контур, по которому будем считать циркуляцию ,следует выбрать прямоугольный. Тогда на участке 1–2 угол , а на участках 2–3 и 4–1 угол . На участке 3–4 (вне соленоида) индукция магнитного поля . Тогда выражение (4) преобразуется в

,

где N – число витков соленоида, охваченных выбранным контуром.

Из выражения (4) следует или

,

где – число витков, приходящихся на единицу длины соленоида.

Экспериментальное изучение распределения магнитной индукции поля внутри соленоида предлагается провести с помощью установки состоящей из источника постоянного тока G; соленоида L₁ магнитное поле которого исследуется; маленькой измерительной катушки L₂, которая введена в соленоид и может перемещаться вдоль его оси; баллистического гальванометра Р₂, соединенного с катушкой L₂; выключателя S и миллиамперметра P₁, с помощью которого можно измерить ток в соленоиде. При измерении индукции магнитного поля измерительную катушку устанавливают в какой-либо точке на оси соленоида. В момент замыкания кнопки S цепи соленоида L₁ ток в нем возрастает от 0 до постоянного значения I . При этом магнитный поток через витки катушки L₂ изменяется от 0 до , где - площадь сечения соленоида, – число витков в катушке L₂. Изменение магнитного потока приводит к возникновению в катушке L₂ электродвижущей силы индукции и появлению в цепи катушки L₂ индукционного тока i. В результате этого световой зайчик гальванометра смещается на угол , пропорциональный количеству электричества , протекшего через измерительную часть установки. Этот угол равен , где b – баллистическая постоянная гальванометра.

Если полное сопротивление цепи электрической катушки L₂ равно R , то ток в ней и поэтому .

Тогда для магнитной индукции имеем или

, (6)

где постоянная принимается за цену деления баллистического гальванометра. По формуле (6) определяются экспериментальные значения магнитной индукции поля на оси соленоида.