
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Теоретическое введение. Тороидальная катушка (тороид) представляет собой провод, навитый на каркас (магнитопровод), имеющий форму тор (рис
Тороидальная катушка (тороид) представляет собой провод, навитый на каркас (магнитопровод), имеющий форму тор (рис. 1). При пропускании тока по плотно навитому проводу образуется магнитное поле, напряженность Н которого вне тороида практически равна нулю, а внутри вычисляется по формуле
Н = IN/l = In, (1)
где I – сила тока, N – полное число витков, n – число витков, приходящееся на единицу длины тороида. Формула (1) справедлива для тороида, длина которого l (l = 2pr) значительно больше, чем диаметр магнитопровода. Можно принять магнитное поле внутри такого тороида однородным.
Индукция магнитного поля В = mm0Н или с учетом (1)
В = mm0nI, (2)
где m – относительная магнитная проницаемость среды (вещества магнитопровода), m0 – магнитная постоянная.
Поток магнитной индукции, сцепленной с тороидом
Ф = Ф0N,
где Ф0 = ВS – поток через один виток тороида площадью S = p d2/4.
Учитывая равенство (2), получаем
Ф = mm0nISN = mm0n2lSI. (3)
Если каркас тороида немагнитный, то поле 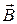 , а значит и полный магнитный поток Ф будут пропорциональны силе тока I, и можно записать
, а значит и полный магнитный поток Ф будут пропорциональны силе тока I, и можно записать
Ф = LI, (4)
где L – коэффициент, называемый индуктивностью тороида. L – физическая величина, численно равная магнитному потоку, сцепленному со всеми витками, когда ток, создающий этот поток, равен единице.
Единицей индуктивности в СИ является генри (Гн). Магнитный поток измеряется в веберах (Вб), причем 1Гн = 1Вб/А.
Сопоставляя выражения (3) и (4), получаем индуктивность тороида
L = mm0n2Sl. (5)
Все вышеизложенное справедливо и для бесконечно длинного соленоида.
При измерении силы тока в тороиде возникает ЭДС индукции, которую называют ЭДС самоиндукции
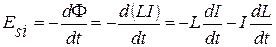 . (6)
. (6)
Если при изменениях силы тока индуктивность остается постоянной (что возможно, когда магнитопровод немагнитный), то ЭДС самоиндукции
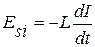 . (7)
. (7)
Соотношение (7) дает возможность определить индуктивность как коэффициент пропорциональности между скоростью изменения силы тока в контуре и возникающей вследствие этого ЭДС самоиндукции. Однако такое определение правомерно лишь в случае, когда L = const.
В присутствии ферромагнетика L будет функцией от I (через Н). Следовательно, dL/dt в формуле (6) можно записать как (dL/dt)(dI/dt). Тогда
 . (8)
. (8)
Отсюда видно, что при наличии ферромагнетика коэффициент пропорциональности между Еsi и dI/dt отнюдь не равен L, как было указано в соотношении (7).
Если магнитопровод тороида изготовлен из ферроипгнитного материала (железа, никеля, кобальта и их сплавов и соединений), то относительная магнитная проницаемость m является сложной функцией от напряженности Н магнитного поля в тороиде (рис.2):
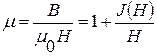 . (9)
. (9)
где J – намагниченность, т.е. магнитный момент единицы объема ферромагнетика. Начиная с некоторого значения Н, численное значение вектора намагниченности практически остается постоянным и равным JН. Это объясняется следующим образом.
При определенных условиях в кристаллах могут возникать так называемые обменные силы, которые заставляют магнитные моменты атомов устанавливаться параллельно друг другу. В результате возникают области (размером 1–10 мкм) спонтанного, т.е. самопроизвольного намагничивания. Эти области называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и имеет определенный магнитный момент. Направления этих моментов для различных доменов различны, поэтому при отсутствии внешнего поля суммарный момент образца равен нулю и образец в целом представляется макроскопически не намагниченным.
При включении внешнего магнитного поля домены, ориентированные по полю, растут за счет доменов, ориентированных против поля. Очевидно, что магнитное насыщение наступает тогда, когда векторы магнитных моментов всех доменов устанавливаются параллельно внешнему магнитному полю.
В относительно слабых полях В растет быстрее Н вследствие быстрого роста J, поэтому m увеличивается до mmax (рис. 2). В сильных полях наступает насыщение намагниченности (J = JН = const), поэтому при дальнейшем росте Н отношение J/H ® 0 и магнитная проницаемость m согласно формуле (9) начинает убывать, стремясь к единице. Следовательно, в сильных магнитных полях индукция В возрастает с увеличением Н по линейному закону (рис. 3).
Если после того, как ферромагнетик намагничен (даже не до насыщения), внешнее магнитное поле устранить, начнется распад крупных доменов на более мелкие. Однако полного хаоса при этом не возникнет и достигнутая намагниченность частично сохранится. Это используют при изготовлении постоянных магнитов. Отметим еще одно свойство ферромагнетиков. Для каждого ферромагнитного вещества существует температура (точка Кюри), выше которой ферромагнитные свойства полностью исчезают и вещество становится парамагнетиком.
В медицине ферромагнетики находят разнообразное применение: исправление грудной клетки у детей, магнитные заглушки для предотвращения выделений из искусственного наружного свища ободочной кишки, для удаления железных частичек из глаз и др.
Итак, m ферромагнетиков является функцией напряженности (или тока, так как Н ~ I). Из формулы (5) видно, что индуктивность тороида зависит от его геометрических размеров и относительной магнитной проницаемости среды. Следовательно, в присутствии ферромагнетика L тороида зависит от I так же, как m от Н. Для немагнитных магнитопроводов m = const, поэтому L = const при изменении тока.
В данной работе в качестве магнитопровода в тороиде используется феррит – материал с магнитными свойствами ферромагнетика, но с низкой (или нулевой) проводимостью.
При прохождении постоянного тока через обмотку тороида он оказывает активное сопротивление R, обусловленное электрическими свойствами проводника, длиной и сечение провода. Если по тороиду пропустить переменный ток, то полное сопротивление тороида возрастает.
Эффективная сила тока в цепи, содержащей индуктивность, емкость и активное сопротивление, определяется формулой
 . (10)
. (10)
где U – эффективное напряжение, XL = wL – индуктивное сопротивление, XC = 1/wС – емкостное сопротивление, 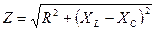 – полное сопротивление цепи (импеданс), w – циклическая частота.
– полное сопротивление цепи (импеданс), w – циклическая частота.
Так как для исследуемого тороида активное сопротивление R мало по сравнению с индуктивным сопротивлением XL, а емкостное сопротивление XC практически отсутствует, то формулу (10) можно записать в виде I = U/wL, откуда
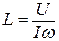 , (11)
, (11)
где w = 2pn, а n = 50 Гц.
Дата добавления: 2014-10-31; просмотров: 542; Мы поможем в написании вашей работы!; Нарушение авторских прав |